How would I use calculus to prove $\arcsin x=\arctan(x/\sqrt{1-x^2})$?

Question

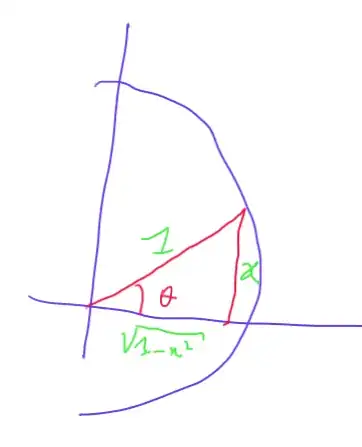
My question is how would I prove the following problem. Im not sure how I would begin. $$\arcsin x=\arctan\frac{x}{\sqrt{1-x^2}},|x|<1$$

Answer 1

A draw is also very good :-)

You can see that $\theta=\arcsin(x)$. But you also have that $$\tan\theta=\frac{x}{\sqrt{1-x^2}}\implies \theta=\arctan\left(\frac{x}{\sqrt{1-x^2}}\right)$$ what prove the claim. By the way, you can also deduce that $$\theta=\arccos(\sqrt{1-x^2})=\arcsin(x)=\arctan\left(\frac{x}{\sqrt{1-x^2}}\right).$$

Answer 2

Usually, when trying to prove function equalities in calculus, you may follow the following procedure:

1. Define $f(x)$, so that what you are going to prove is $f(x)=0$. 5 sO in your case let $f(x) = \arcsin(x) - \arctan(\frac{x}{\sqrt{1-x^2}})$ .

2. Compute $f'(x)$ and try to show $f'(x)=0$. Then your $f(x) $ is constant. (and this is the case in your question)

3. Calculate $f(a)$ for some $a$ in the domain you have, to find that $f(a)=0$, and as $f$ is constant, then $f(x)=0$ for all $x$ in your domain. (in your case try $f(0)$).

Answer 3

HINT:

$$\dfrac{d(\arctan x/\sqrt{1-x^2})}{dx}$$

$$=\dfrac1{1+x^2/(1-x^2)}\left(\dfrac1{\sqrt{1-x^2}}-\dfrac12\dfrac x{(1-x^2)^{3/2}}(-2x)\right)$$

$$=\dfrac{(1-x^2)(1-x^2+x^2)}{(1-x^2+x^2)(1-x^2)^{3/2}}=?$$

Answer 4

Note that $$\arcsin (X)=\alpha$$ means simply that $$\sin \alpha=X$$ and $$\arctan (Y)=\alpha$$ means $$\tan \alpha=Y$$ so your equation means: $$ \tan \alpha=\dfrac{\sin \alpha}{\sqrt{1-\sin^2 \alpha}}= \dfrac{\sin \alpha}{\cos \alpha} $$