I am struggling to show that $$\dfrac \pi{2\sqrt3}=1-\dfrac 15+\dfrac 17-\dfrac 1{11}+\dfrac 1{13}-\dfrac 1{17}+\dfrac 1{19}-\cdots$$ by using the Fourier series $$\frac \pi2-\frac x2=\sum_1^\infty \dfrac {\sin(nx)}{n}.$$
Can somebody give me any hint?
My first thought did not use the identity in the question, but used identity $(7)$ proven in this answer, $$ \sum_{k\in\mathbb{Z}}\frac1{z+k}=\pi\cot(\pi z)\tag{1} $$ so that $$ \begin{align} \sum_{k\in\mathbb{Z}}\frac1{1+6k} &=\frac16\sum_{k\in\mathbb{Z}}\frac1{\frac16+k}\\ &=\frac16\pi\cot\left(\frac\pi6\right)\\[6pt] &=\frac\pi6\sqrt3\\[6pt] &=\frac\pi{2\sqrt3}\tag{2} \end{align} $$
To use the identity in the question, $$ \frac\pi2-\frac x2=\sum_1^\infty\frac{\sin(nx)}n\tag{3} $$ it appears that we could consider $x=\frac\pi3$: $$ \begin{align} \frac\pi2-\frac\pi6 &=\sum_{n=1}^\infty\frac{\sin\left(\frac{n\pi}3\right)}{n}\\ &=\frac{\sqrt3}2\left(\color{#C00000}{\frac11}\color{#0000F0}{+\frac12-\frac14}\color{#C00000}{-\frac15+\frac17}\color{#0000F0}{+\frac18-\frac1{10}}\color{#C00000}{-\frac1{11}+\frac1{13}}+\dots\right)\\ &=\frac{\sqrt3}2(\color{#C00000}{A}+\color{#0000F0}{B})\tag{4} \end{align} $$ Note that the sum we seek is $A$. It is an easy exercise to verify that the series for both $A$ and $B$ converge (using The Alternating Series Test).
Now we have that $(A+B)+2B=2A$: $$ \begin{array}{rl} \displaystyle A+B=&\displaystyle\frac11+\frac12-\frac14-\frac15+\frac17+\frac18-\frac1{10}-\frac1{11}+\frac1{13}+\dots\\ \displaystyle 2B=&\displaystyle\frac11-\frac12+\frac14-\frac15+\frac17-\frac18+\frac1{10}-\frac1{11}+\frac1{13}+\dots\\ \displaystyle 2A=&\displaystyle\frac21\phantom{+\frac02-\frac04}\ \ -\frac25+\frac27\phantom{+\frac08-\frac0{10}}\ \ -\frac2{11}+\frac2{13}+\dots\tag{5} \end{array} $$ Thus, $A=3B$. Using this in $(4)$ gives $$ \frac\pi3=\frac{\sqrt3}2\left(A+\frac13A\right)\tag{6} $$ and solving for $A$ yields $$ A=\frac\pi{2\sqrt3}\tag{7} $$
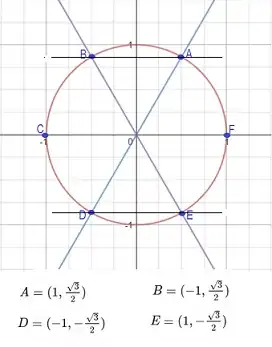
In the figure below, in which the trigonometric circle has been divided into six equal parts, we can see clearly that for $x= \frac {\pi}{3}$ the following equalities are verified:
$\sin( \frac{n\pi}{3})=\frac{\sqrt3}{2}$ for $n=1,2,7,8,……, 1+6n,2+6n,…..$
$\sin( \frac{n\pi}{3})=\frac{-\sqrt3}{2}$ for $n=4,5,10,11,......,4+6n,5+6n$
$\sin\left( \frac{n\pi}{3}\right)=0$ for $n=3,6,9,12,……,3n$
Hence, for $x= \frac {\pi}{3}$
$$\frac {\pi}{2} - \frac {\pi}{6}=\frac{\pi}{3}$$
$$\frac{\pi}{3}=\frac{\sqrt 3}{2}\sum_{n=1}^\infty \left[\frac{1}{1+6n} +\frac{1}{2+6n}-\frac{1}{4+6n}-\frac{1}{5+6n}\right]$$ We have $$\frac{\pi}{3}=\frac{\sqrt 3}{2}A\iff \frac{\pi}{2\sqrt3}=\frac{3}{4}A=(1-\frac14)A$$ From which we see the odd-denominator terms $$\frac{1}{1+6n} -\frac{1}{5+6n}$$ remain unchanged and the even-denominator terms $$\frac{1}{2+6n} -\frac{1}{4+6n}-\frac{1}{4+24n}-\frac{1}{8+24n}+\frac{1}{16+24n}+\frac{1}{20+24n}$$
give a telescopic series of total sum equal to zero.
(Note that $4+24n=4+6(4n)$;$8+24n=2+6(4n+1)$; $16+24n=4+6(4n+2)$;$20+24n=2+6(4n+3)$; we obtain $$0=\frac12-\left(\frac14+\frac14\right) = \frac18-\frac18=\frac{1}{10}-\left(\frac{1}{20}+\frac{1}{20}\right)=\frac{1}{14}-\left(\frac{1}{28}+\frac{1}{28}\right)$$ an so on.
Thus we end with the addition of the terms $$\frac{1}{1+6n} -\frac{1}{5+6n}$$
The approach we take is to find a discrete and finite Fourier-series of the periodic sequence $f(n)$ in the sum $\sum\frac{f(n)}{n} = \frac{\color{red}{1}}{1} + \frac{\color{red}{0}}{2} + \frac{\color{red}{0}}{3} + \frac{\color{red}{0}}{4} + \frac{\color{red}{-1}}{5} + \frac{\color{red}{0}}{6} \ldots$ we are trying to compute. This will allow us to use this (finite) Fourier series in combination with the Fourier series in the question to evaluate the sum.
Consider the function $f:\mathbb{N}\to\mathbb{N}$ given by (which is the Dirichlet character modulo $6$ hinted to by Paul in the comments)
$$f(n) = \left\{\matrix{0 & n\equiv 0\mod 6\\1 & n\equiv 1\mod 6\\0 & n\equiv 2\mod 6\\0 & n\equiv 3\mod 6\\0 & n\equiv 4\mod 6\\-1 & n\equiv 5\mod 6}\right.$$
This function is constructed such that your series can be written as
$$1 - \frac{1}{5} + \frac{1}{7} - \frac{1}{11} + \frac{1}{13} - \ldots = \sum_{n=1}^\infty \frac{f(n)}{n}$$
Since $f$ is periodic with period $6$ it has a Fourier series
$$f(n) = \sum_{k=0}^5c_k \sin\left(\frac{2\pi k}{6}n\right)$$
where the coefficients are given by
$$c_k = \frac{1}{6}\sum_{j=0}^5f(j)\sin\left(\frac{2\pi k}{6}j\right) = \frac{\sin\left(\frac{\pi k}{3}\right)-\sin\left(\frac{5\pi k}{3}\right)}{6}$$
The sum you are after can therefore be written as
$$\sum_{n=1}^\infty\frac{f(n)}{n} = \sum_{k=0}^5c_k \color{red}{\sum_{n=1}^\infty\frac{\sin\left(\frac{2\pi k}{6} n\right)}{n}} = \sum_{k=0}^5c_k\color{red}{\left(\frac{\pi}{2} - \frac{\left(\frac{2\pi k}{6}\right)}{2}\right)}$$
where we have used the Fourier series in the question to evaluate the infinite sums. This gives the desired result
$$\sum_{n=1}^\infty \frac{f(n)}{n} = \sum_{k=0}^5\frac{\sin\left(\frac{\pi k}{3}\right)-\sin\left(\frac{5\pi k}{3}\right)}{6} \frac{(3-k)\pi}{6} = \frac{\pi}{2\sqrt{3}}$$
The method we used above generalises to computing the sum of any series $\sum \frac{f(n)}{n}$, where $f(n)$ is a periodic function (with integer period).
This sum may be tackled using the residue theorem.
$$S=\sum_{k=0}^{\infty} \left ( \frac1{6 k+1} - \frac1{6 k+5}\right ) = \frac12 \sum_{k=-\infty}^{\infty} \left ( \frac1{6 k+1} - \frac1{6 k+5}\right )$$
Thus, consider the contour integral
$$\oint_{C_N} dz \frac{2 \pi \, \cot{\pi z}}{36 \left (z+\frac16\right ) \left (z+\frac{5}{6}\right )} $$
where $C_N$ is the square with vertices at $z =\pm (N \pm 1/2)$. As $N \to \infty$, the integral is zero. Thus the sum of the residues at the poles $z=k, k \in \mathbb{Z}$ and $z=-1/6$ and $z=-5/6$ is zero. We thus have
$$\sum_{k=0}^{\infty} \left ( \frac1{6 k+1} - \frac1{6 k+5}\right ) =-\frac{\pi}{18} \left [\frac{\cot{\left ( -\frac{\pi}{6} \right )}}{\frac{4}{6}} + \frac{\cot{\left ( -\frac{5 \pi}{6} \right )}}{-\frac{4}{6}} \right ] = 2 \sqrt{3} \frac{\pi}{18} \cdot \frac{3}{2} = \frac{\pi}{2 \sqrt{3}}$$
