1

I found myself intrigued by the result of the definite integrals of $\frac{1-x}{x}$ and $\sqrt{\frac{1-x}{x}}$ respectively. Both functions are seemingly similar, with vertical asymptotes at $x=0$. However the area bounded between the two and the $x$-axis for $x=[0,1]$ is clearly different. Let $f(x)=\frac{1-x}{x}$:

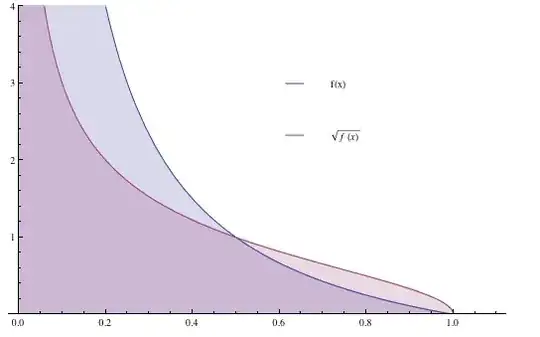
                     graph of f(x) and sqrt(f(x))

and so we have: $$ \begin{align} &\int\limits^{1}_{0}f(x)\,dx=\infty\\ &\int\limits^{1}_{0}f(x)^{1/2}\,dx=\frac{\pi}{2} \end{align} $$

Now, since $\displaystyle\lim\limits_{x\to0}\,f(x)=\lim\limits_{x\to0}\,f(x)^{1/2}=\infty$ shouldn't the two both evaluate to infinity? Even though it is clear that $\int\limits^{1}_{0}f(x)^{1/2}\,dx$ will be less than $\int\limits^{1}_{0}f(x)\,dx$, how can that be that one evaluates to infinity while the other to merely $\approx1.57\!\!\ldots$?

Has this something to do with this? Or perhaps with the fact that $\ln{x}$, which forms a part of the indefinite integral for $f(x)$, isn't defined for $0$?

Community
  • 1
Milo Wielondek
  • 1,919
  • 2
    Perhaps you'd look at a simpler example of the same phenomenon, the integrals of $1/x$ and $1/\sqrt x$. Without the clutter, you might see what's going on. – Gerry Myerson May 16 '12 at 00:04
  • @GerryMyerson Indeed, the two cases are very similar, which is also why considering the other case didn't lend me any more insight. It still doesn't make a lot of sense to me. – Milo Wielondek May 16 '12 at 11:43
  • Intuitively, you can think of the graph of $\sqrt{\frac{1-x}{x}}$ as "hugging" the y-axis "tighter" than $\frac{1-x}{x}$ does. – The_Sympathizer May 23 '13 at 04:20

2 Answers2

7

Well, this is not that different from what happens with some infinite series: $$\sum_{n=1}^\infty\frac{1}{n}=\infty$$ $$\sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}$$ and, in fact, the explanation is somehow similar.

DonAntonio
  • 211,718
  • 17
  • 136
  • 287
  • I was after an explanation, not another special case, but thanks. Now, what is the explanation? – Milo Wielondek May 16 '12 at 11:37
  • I don't know what you would accept as an "explanation". The two graphs are unbounded. Whether they enclose a finite or an infinite area depends on how fast they rise, just as whether DonAntonio's series converge or diverge depends on how fast the terms fall. If the graphs rise too fast (if the terms in the series fall too slowly), the integral (sum) diverges. If the graph rises slowly enough (if the terms fall quickly enough), the integral (sum) converges. It doesn't matter that, in some sense, the functions look similar; 65536 and 65537 look similar, one is prime, one is a power of two. – Gerry Myerson May 16 '12 at 12:50
  • @GerryMyerson are you saying we should accept this as a (counter-intuitive) fact? Something akin to the harmonic series? – Milo Wielondek May 16 '12 at 16:28
  • Some people would say the convergence of $\int_0^1(1/\sqrt x),dx$ and $\sum^{\infty}n^{-2}$ are the counter-intuitive facts. But of course we don't "accept" anything - we give a proof. But maybe I misunderstand your question. – Gerry Myerson May 16 '12 at 22:42
  • @GerryMyerson and the proof in this case is given simply by evaluating the integral? – Milo Wielondek May 17 '12 at 08:50
  • Yes. ${}{}{}{}$ – Gerry Myerson May 17 '12 at 11:27
1

One has that

$$\int_0^1 \frac {1-x} {x } dx =\left. \log x -x \right|_0^1\to \infty$$

Whereas

$$\int_0^1 \sqrt{\frac {1-x} {x }} dx =$$

$$x=\sin^2 \theta$$

$$dx=2 \sin \theta \cos \theta$$ $$\int_0^{\frac{\pi }{2}} {\sqrt {\frac{{1 - {{\sin }^2}\theta }}{{{{\sin }^2}\theta }}} } 2\sin \theta \cos \theta = 2\int_0^{\frac{\pi }{2}} {{{\cos }^2}\theta } = 2\frac{\pi }{4}=\frac{\pi }{2}$$

There is not much more explanation than that. One evaluates in terms of the logarithm, so it diverges. For the other, an idea would be to look at inverses.

The inverse of the latter is $$\frac{1}{{1 + {x^2}}} = y$$ which is well beaved in the real realm. Actually, you're computing

$$\int\limits_0^\infty {\frac{1}{{1 + {x^2}}}dx} = \int_0^1 {\sqrt {\frac{{1 - x}}{x}} } dx = \frac{\pi }{2}$$

Pedro
  • 122,002