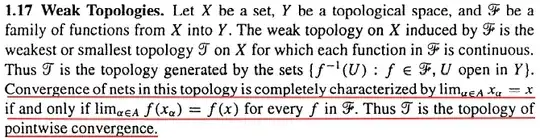In general we have the following definition of initial (or weak) topology: given a set $X \neq \varnothing$, a family of topological spaces $\{ (Y_i, \tau_i ) \}_{i \in I}$, and for every $i \in I$ a function $f_i : X \to Y_i$, the initial (or weak) topology is the weakest topology on $X$ that makes all the functions $f_i$ continuous.
Take the set $\mathcal{F} := \{ f \ | \ f \in \mathbb{R}^X \}$, and notice that the weak topology on $\mathcal{F}$, denoted by $\sigma (\mathcal{F}, X)$, is identical to the relative topology on $\mathcal{F}$ as subset of $\mathbb{R}^X$ endowed with the product topology.
Moreover, notice that, given our definition of $\mathcal{F}$, the set $X$ can be seen as set of real valued functions on $\mathcal{F}$, where each $x \in X$ can be seen as an evaluation functional $e_x \in \mathbb{R}^\mathcal{F}$ such that $e_x (f) = f(x)$, i.e. $X = \{ \ e_x \ | \ e_x \in \mathbb{R}^\mathcal{F}, \ e_x (f) = f(x) \ \}$
Now, let $X$ a linear space with $x \in X$. Thus, let $X’$ be the algebraic dual of $X$, i.e. the vector space of all linear functionals on $X$, and let $X^*$ be the topological dual of $X$, i.e. $$X^* := \big\{ x^* \ \big| \ x^* \in \mathbb{R}^X, \ x^* \text{ continuous} \big\},$$ or – in plain english – the vector space of all continuous linear functionals on $X$, with $x^* \in X^*$.
Notationally wise, notice that, for the following, (for example) Rudin writes $\langle x , x^* \rangle \equiv x^*(x)$, thus (according to the notation employed above) we should have that $\langle x^* , x \rangle \equiv e_x (x^*)$.
Hence, $X$ can be seen (like in the second paragraph) as a vector subspace of $\mathbb{R}^{X^*}$, in which case $\sigma (X, X^*)$ is the weak topology on $X$ (denoted by $w$), defined as
$$ x_\alpha \overset{w}{\to} x \in X \Longleftrightarrow \forall x^* \in X^* , \langle x_a, x^* \rangle \to \langle x , x^* \rangle \in \mathbb{R}, $$
that corresponds to the topology of pointwise convergence on $X^*$.
In the same vein, $X^*$ can be seen as a vector subspace of $\mathbb{R}^X$, in which case $\sigma (X^*, X)$ is the weak* topology on $X^*$ (denoted by $w^*$), defined as
$$ x^{*}_\alpha \overset{w^*}{\to} x^* \in X^* \Longleftrightarrow \forall x \in X , \langle x^{*}_a, x \rangle \to \langle x^* , x \rangle \in \mathbb{R}. $$
Notice that in both cases we are just declining in different ways the original definition of initial topology given at the beginning. What we are changing is simply the "reference" space that makes all functions continuous:
- In the case of the weak topology, we have that $(X, \sigma(X, X^*))$ is the topological space that makes all the $x^* \in X^*$ continuous;
- In the case of the weak* topology, we have that $(X^*, \sigma(X^*, X))$ is the topological space that makes all the evaluation functionals $e_x \in \mathbb{R}^{X^*}$ continuous.
In light of what above, the one you were expecting is the weak*-topology, and not the weak-topology. Interestingly, and here we get to the all problem of the topology of pointwise convergence, we can endow different spaces with that topology. In my answer (and in your book), the space endowed with that topology is $X^*$, while – most probably – your problem arose because instead you had in mind $X$ endowed with that topology.