1

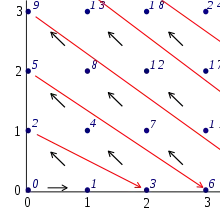
I know a function like this exists but I'm not able to find it.

It's not the same as g(x,y) = 2^{x-1} (2y-1) which is used to prove the same thing for naturals because here we want x to be a positive or negative integer. So that function can't be used.

maria
  • 19
  • How do you know it exists? – Marra Sep 27 '15 at 14:46
  • 1
    @Marra: a finite product of countable sets is countable. – Bernard Sep 27 '15 at 14:47
  • I was thinking about a real, continuous function since it was tagged as a Real Analysis question. Totally missed the countability of them. – Marra Sep 27 '15 at 14:49
  • My favorite example of a bijection between these two sets involves a spiral path starting from 0. – Patrick Tam Sep 27 '15 at 14:54
  • You can use a one-to-one and onto function $\Bbb Z\to\Bbb N$ to adapt the approach from the link Najib posted. – Cameron Buie Sep 27 '15 at 15:02
  • I'm not sure I understand what you mean @CameronBuie – maria Sep 27 '15 at 15:08
  • @maria: If you have a one-to-one function $f:\mathbb{Z} \to \mathbb{N}$, and a one-to-one function $g:\mathbb{N}\times \mathbb{N} \to \mathbb{N}$, then one easily shows that $f^{-1}(g(f(m),f(n)))$ gives a one-to-one function from $\mathbb{Z}\times \mathbb{Z}$ onto $\mathbb{Z}$. Note that one-to-one functions are commonly defined as being both one-one (injective) and onto (surjective). – hardmath Sep 27 '15 at 15:48

4 Answers4

3

First, write a sequence with all the elements of $\Bbb Z\times \Bbb Z$: $$(0,0),(1,0),(0,1),(-1,0),(0,-1),(2,0),(1,1),(0,2),(-2,0),(-1,-1),(0,-2),(1,-1),(-1,1),\ldots$$

Now do the same with $\Bbb Z$: $$0,1,-1,2,-2,3,-3,\ldots$$

Finally just define a function that associates the first with the first, the second with the second, etc.

ajotatxe
  • 65,084
1

enter image description here

Have a look to the picture. From it you may be able to define the required map. Just need some computation. The map is very instructive to understand what happens.

mathcounterexamples.net
  • 70,018
  • Nice visualization. Though this should be modified to map from $\mathbb{Z} \times \mathbb{Z}$ and not from $\mathbb{Z}{\ge 0} \times \mathbb{Z}{\ge 0}$... – Tintarn Sep 27 '15 at 14:52
0

There is a non-constructive proof from the Cantor-Schroder-Bernstein Theorem, because we can find one-to-one functions in both directions.

The hard direction is as follows. Let $(m,n)\in\mathbb{Z}\times\mathbb{Z}$. If $m,n\ge 0$, then map it to $2^m3^n$. If $m<0,n\ge 0$, then map it to $5^m3^n$. If $m\ge 0, n<0$, then map it to $2^m7^n$. Lastly, if $m,n<0$, then map it to $5^m7^n$.

vadim123
  • 82,796
  • I was just about to say "an unhelpful answer would be to step through the Schroeder-Bernstein theorem". I know a constructive proof of that theorem, so this does actually produce an example, but it's really unwieldy. – Patrick Stevens Sep 27 '15 at 14:48
0

One way is to take $(a, b)$ to $$2^{\vert a \vert} 3^{\vert b \vert} 5^{\overline{\text{sgn}}(a)} 7^{\overline{\text{sgn}}(b)}$$

where $\overline{\text{sgn}}(a)$ is $1$ if $a>0$, $0$ if $a \leq 0$. Then biject those with the integers in alternating order, which we can now do easily because the image of the above map is well-ordered. $$1 \mapsto 0, 2 \mapsto 1, 3 \mapsto -1, 4 \mapsto 2, 5 \mapsto -2, \dots, 10 \mapsto f(10), 12 \mapsto f(12), \dots$$

Patrick Stevens
  • 36,135