Simson line: Does reflection preserve collinearity?

Question

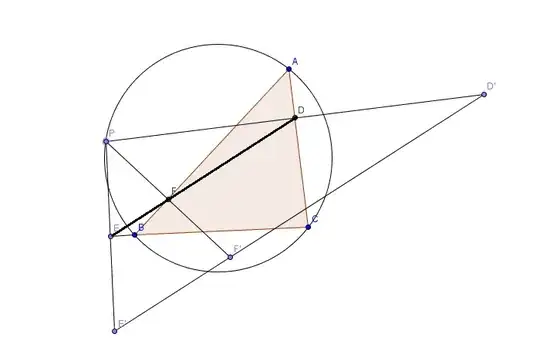
It is known that for any triangle $ABC$, we can construct a circle that circumscribes it. Let $P$ be a point on this circle that does not coincide with the vertices of triangle $ABC$.

By playing around with a few diagrams, I noticed that by reflecting $P$ in the sides of the triangle, it seems to me that I get a set of three collinear points.

Is my guess actually a theorem, or is it just plain wrong? In the case that it is actually true, then how would one go from the Simson line to deducing that the reflections are also collinear? I suspect there may be a relationship between the two concepts.

There's already an answer of @anachor, but see also this post, where I derive the existence of Simson line from collinearity of reflections. — dtldarek, Sep 24 '15 at 12:05

score 2 · Accepted Answer · edited Jun 12 '20 at 10:38

2

Do you know homothety? Then your observation is just a homothety away from simson line.

In the diagram above $DEF$ is the simson line. Apply an homothety with center P and ratio $2$ and Voila! $D'E'F'$ is a straight line too.

In other words the ratios $PD \over PD'$ = $PE \over PE'$ = $PF \over PF'$ =$0.5$. Since D,E,F are collinear, so are D', E', F'

edited Jun 12 '20 at 10:38

Community

1

answered Sep 24 '15 at 11:57

Rohcana

449

Yes I do know it. That makes complete sense. Thank you. – Trogdor Sep 24 '15 at 11:57

Simson line: Does reflection preserve collinearity?

1 Answers1