Trigonometric functions $\cos$ and $\sin$ are related to points on the unit circle: they are the $x$ and $y$ coordinates.
Is there such a relation for $\cosh$ and $\sinh$, hyperbolic functions? What would play the role of the unit circle here, and how would the function be obtained from it?
Normally we think of an angle in terms of arc length. But, an alternative to define an angle as twice the area (within the unit circle) swept by the terminal side as it moves away from the initial side. Note that a unit circle has area and circumference of $\pi\cdot 1^2=\pi$ and $2\pi\cdot 1=2\pi$, respectively, so the arc length and area of any sector area linearly related (i.e. the arc length is always twice that of the area).
We can define a hyperbolic "angle" similarly, as twice the area swept from the initial side to the terminal side on the hyperbola $x^2-y^2=1$.
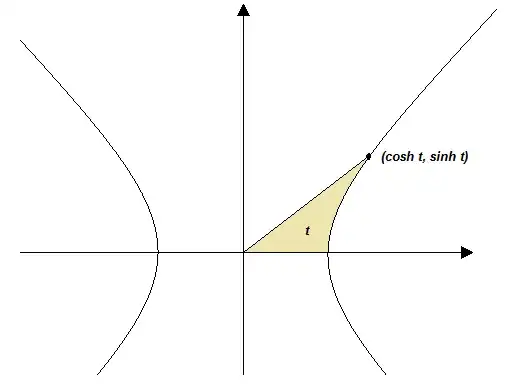
You really need integral calculus to find $\sinh t$ and $\cosh t$ in terms of $t$, so I'll leave that as a fun project for you. :) Oh, and don't forget to derive the formulas for arsinh and arcos too; they're even more fun.
