0

Can someone help me out? I don't really get what "x does not belong to x" means in this: 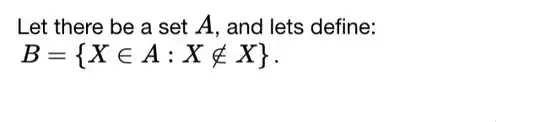Russel's paradox

drhab
  • 151,093
user265554
  • 2,853
  • Related: http://math.stackexchange.com/questions/253818/example-of-set-which-contains-itself – Asydot Sep 21 '15 at 14:14
  • 1
    It means that $X$ is not element of $X$. – drhab Sep 21 '15 at 14:17
  • If you are wondering how a set can be element of itself, it is a construct that you will never see in, say, number theory or analysis. It is one, however, that created chaos in set theory just over a century ago, and inspired various "fixes" to set theory. There was no formally stated rule that you could not have $x\in x$ or $x\notin x$. So why not have $S={x:x\notin x}$? This led to Russell's famous paradox. You could both prove and disprove the existence of $S$ using the set theory of the day. – Dan Christensen Sep 21 '15 at 15:26

1 Answers1

0

In this scheme, the elements $X$ of $A$ may themselves be sets. In fact, the set $X$ might contain itself as an element, so that $X \in X$. For example, a set $Y$ satisfying $Y = \{1,2,Y\}$ contains itself.

What we are defining, then, is the set of elements $X$ (of $A$) that do not contain themselves. In particular, if we take $Y$ as defined above, then $Y \notin B$.

Ben Grossmann
  • 225,327
  • I should rather say: a set $Y$ that satisfies $Y={1,2,Y}$ contains itself (as element). – drhab Sep 21 '15 at 14:32
  • @drhab is the set not uniquely determined by this equality? – Ben Grossmann Sep 21 '15 at 14:36
  • I don't think so. Am I wrong then? My comment was purely based on intuition. Btw, got to go now. I will come back later. – drhab Sep 21 '15 at 14:43
  • I say that $Y$ is uniquely described since we have given all of its elements. – Ben Grossmann Sep 21 '15 at 14:45
  • @Omnomnomnom It depends on your set theory. In ZF set theory, there is no such $Y$. In Peter Aczel's set theory your intuition is correct and there is a unique set $Y$ with the property you describe. – MJD Sep 21 '15 at 14:46
  • @MJD My thoughts are as follows: regardless of one's choice of set theory, the axiom of extensionality grants us that if such a set exists, then it is unique. – Ben Grossmann Sep 21 '15 at 14:50
  • 1
    I don't see where you get that. Suppose the property $Y = {1,2,Y}$ holds for two different entities, say $y_1$ and $y_2$. You want to claim based on extensionality that $y_1=y_2$ because they have the same elements, but to do that you need to know $y_1=y_2$ already. – MJD Sep 21 '15 at 15:49
  • @MJD you have me there; I didn't really think it through. – Ben Grossmann Sep 21 '15 at 15:50