Understanding the Unit Circle

Question

I'm going to need to know this (the unit circle, English) for a test, but I'm so horrible with both charts and memorization, the whole thing is failing to stick into my brain. Using non-complicated English (literally, I could be the dumbest person here [at least I admitted it, so be kind Dx]), is there a mnemonic (I know, numbers and English), a list, some ridiculously easy hack for this??

Answer 1

I use a "ridiculously easy" trick to memorize trigonometric values of angles:

There are 5 angles primarily used from the unit circle: 0, 30, 45, 60, 90. This trick will provide the sine, cosine and tangent values for all 5.

Sine

1) Start by writing out the numbers 0 to 4 in ascending order: $0, 1, 2, 3, 4$

2) Divide all values by 4: $\frac{0}{4}, \frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \frac{4}{4}$

3) Simplify all fractions: $0, \frac{1}{4}, \frac{1}{2}, \frac{3}{4}, 1$

4) Square root the numerators and denominators: $\left(\sqrt 0\right), \left(\frac{\sqrt(1)}{\sqrt(4)}\right), \left(\frac{\sqrt(1)}{\sqrt(2)}\right), \left(\frac{\sqrt(3)}{\sqrt(4)}\right), \left(\sqrt{1}\right)$

5) Simplify the fractions: $0, \left(\frac{1}{2}\right), \left(\frac{1}{\sqrt(2)}\right), \left(\frac{\sqrt(3)}{2}\right), 1$

And the resulting values are your sine values in ascending degree order:

$\sin 0 = 0 $

$\sin 30 = \left(\frac{1}{2}\right)$

$\sin 45 = \left(\frac{1}{\sqrt(2)}\right) $ This can be rationalized to $\left(\frac{\sqrt(2)}{2}\right)$ by multiplying by $\left(\frac{\sqrt(2)}{\sqrt(2)}\right)$

$\sin 60 =\left(\frac{\sqrt(3)}{2}\right)$

$\sin 90 = 1 $

Cosine

Your cosine values are the same fractions above, but in descending degree order. (reverse order of sine)

$\cos 0 = 1 $

$\cos 30 = \left(\frac{\sqrt(3)}{2}\right)$

$\cos 45 = \left(\frac{1}{\sqrt(2)}\right) $ This can be rationalized to $\left(\frac{\sqrt(2)}{2}\right)$ by multiplying by $\left(\frac{\sqrt(2)}{\sqrt(2)}\right)$

$\cos 60 =\left(\frac{1}{2}\right)$

$\cos 90 = 0 $

Tangent

$\tan\theta = \frac{\sin\theta}{\cos\theta}$

Therefore the tangent of any angle can be figured out by dividing the sine of that angle by the cosine of that angle.

Cotangent, Cosecant, Secant

These are simply the inverses of the tangent, sine and cosine of an angle.

Answer 2

$$\begin{array}{c|ccccc} & \;\;0^\circ & \;\;30^\circ\;\; & \;\;45^\circ\;\; &\;\; 60^\circ\;\; & \;\;90^\circ\\[0.1in]\hline \sin & \frac{\sqrt{0}}{2} & \frac{\sqrt{1}}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & \frac{\sqrt{4}}{2}\\[0.1in]\hline \cos & \frac{\sqrt{4}}{2} & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{1}}{2} & \frac{\sqrt{0}}{2} \end{array}$$

Answer 3

Here's how I know the common trig values (I'm assuming this is what you're looking for - hard to make out from your post):

Simply remember that $\sin(0) = 0$. Since $\sin(0) = 0, \cos(0)$ must equal $1.$ Also, it is easy to see that $\sin(30) = \frac{1}{2}$ by drawing a picture. At this point, I know in order to get a hypotenuse of $1$ (for the unit circle), you could deduct that $\cos(30) = \frac{\sqrt3}{2}$ by using the Pythagorean Theorem. Here, now note that $\sin$ and $\cos$ alternate or "flip" for lack of a complicated word (complement!). What I mean by this is that, $\sin(60) = \frac{\sqrt3}{2} = \cos(30)$ and $\cos(60) = \frac{1}{2} = \sin(30)$.

Also, for $45$ degrees, it should be easy to see that both $\sin$ and $\cos$ need to be $\frac{\sqrt2}{2}$ since our hypotenuse is $1$ for a unit circle.

Alternative way:

$\sin (\theta)$ for $0, 30, 45, 60, 90$ degrees follows the order of:

$$\frac{\sqrt{0}}{2}, \frac{\sqrt{1}}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, \frac{\sqrt{4}}{2}$$

For $\cos(\theta)$, it is simply the reverse.

Also, if you're having troubles with what function is positive in what quadrant, I suggest the simple tool I learned in school: ASTC (all students take calculus). All functions are positive in the first quadrant, only $\sin$ is positive in the second quadrant, only $\tan$ is positive in the third, and only $\cos$ is positive in the fourth quadrant.

Answer 4

Assuming you are talking about values of the trig functions at typical "special" angles (where the angle measure and the values of the trig functions are relatively simple), I tend to keep track of the values based on three facts:

• $(\cos\theta,\sin\theta)$ is the rotation image of $(1,0)$ by $\theta$ about the origin—that is, the cosine and sine of an angle are, respectively, the $x$- and $y$-coordinates of the point on the unit circle.
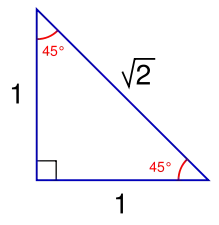
• The sides of a 45°-45°-90° triangle are in the ratio $1:1:\sqrt{2}$. (diagram from wikipedia)
  
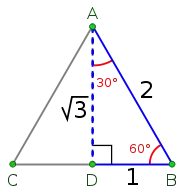
• The sides of a 30°-60°-90° triangle (outlined in blue, half of an equilateral triangle) are in the ratio $1:\sqrt{3}:2$. (diagram from wikipedia)
  

To figure out the cosine and sine of a special angle:

1. find the corresponding point on the unit circle
2. if the point is on the $x$- or $y$-axis, no triangles needed
3. otherwise, place a triangle similar to one of the two triangle from above inside the unit circle so that the hypotenuse is a radius of the circle and one leg lies on the $x$-axis (not the $y$-axis); since we're working in the unit circle, the sides will be $\frac{1}{2}$, $\frac{\sqrt{3}}{2}$, and 1 or $\frac{1}{\sqrt{2}}$, $\frac{1}{\sqrt{2}}$, and 1.
4. if the point is not in the first quadrant, add negative signs to the legs as needed (if the leg/legs is/are in the negative $x$- or $y$-direction)
5. read off the cosine and sine as the $x$- and $y$-coordinates, which are the legs of the triangle with negative signs inserted as needed.

If you need one of the other trig functions, find the sine and cosine and use those to calculate the other trig function.

Answer 5

The easiest way I learned to memorize the unit circle is using your hand.

Hold out your right hand palm up. Assign 0 degrees, 30, 45, 60, and 90 to your fingers, starting with your thumb. To remember the values for sine and cosine, simply lower the finger representing the angle you want. The remaining fingers help you remember the values you need. Fingers to the left of the finger that's lowered tell you the rooted number over 2 for the cosine, fingers to the right of the lowered finger tell you the rooted number over 2 for the sine. You may have to simplify.

Example: 30 degrees. Lower your index finger. To the left of index finger, you have 3 fingers >> root3/2 is the cosine value. To the right of index finger, you have 1 finger >> root1/2 (which simplifies to 1/2).

This method is easiest for first quadrant but you can modify it for all 4. This helped me when I forgot some of the values.

Full explanation https://geometrycoach.com/the-unit-circle-hand-trick/