My goal is to prove that:
$\displaystyle\sum\limits_{n=1}^\infty \frac{1}{n^{x}} \rightarrow \infty$ for all $ x\rightarrow 1^+$
In order to show this statement I show that no matter how big you choose $N\in \mathbb{R}$, you can always find a $\delta >0$ so $\displaystyle\sum\limits_{n=1}^\infty \frac{1}{n^{x}} = 1+\frac{1}{2^{x}}+\cdots+0>N$ when $x\in \left]1,1+\delta\right[$
My idea is to use some kind of "induction".
First/the start : N = 1.25
If we look at the case where $N = 1.25$ I conclude that i can just choose $\delta = 1$ so the following statement is true:
$\displaystyle\sum\limits_{n=1}^\infty \frac{1}{n^{x}} = 1+\frac{1}{2^{x}}+\cdots+0> 1.25$ for all $x\in \left]1,2\right[$
The "induction"-step
I now assume that the following statement is true for an $N$:
There exists a $\delta>0$ so
$\displaystyle\sum\limits_{n=1}^\infty \frac{1}{n^{x}} = 1+\frac{1}{2^{x}}+\cdots+0>N$ for all $x\in \left]1,1+\delta\right[$
Now I multiply the above equation with $x$ ($x$ is greater than $1$)
$\displaystyle x+\frac{x}{2^{x}}+\frac{x}{3^{x}}+\cdots +0>xN$ for all $x\in \left]1,1+\delta\right[$
Then I do some magic and get from the above:
$\displaystyle 1+\frac{x}{2^{x}}+\frac{x}{3^{x}}+\cdots+0>xN-x+1$ for all $x\in \left]1,1+\delta\right[$
I now see that following is true:
$xN-x+1 > N$
Because I dont need to go below $N=1.25$ and can therefore do the following calculations:
$xN-x+1 = x(N-1)+1> N \Leftrightarrow \\ x(N-1)>N-1 \Leftrightarrow \\ x>1$
From all this I can finally conclude that:
$\displaystyle 1+\frac{x}{2^{x}}+\frac{x}{3^{x}}+\cdots+0>xN-x+1>N$ for all $x\in \left]1,1+\delta\right[$
I now write the above as:
$1+\dfrac{1}{2^{x-\frac{\ln(x)}{\ln(2)}}}+\dfrac{1}{3^{x-\frac{\ln(x)}{\ln(3)}}}+\cdots+0>xN-x+1>N$ for all $x\in \left]1,1+\delta\right[$
Because I can use the following true statement:
$\dfrac{1}{x} = a^{-\frac{\ln(x)}{\ln(a)}}$
From the above I can get a new statement:
$1+\dfrac{1}{2^{x-\frac{\ln(x)}{\ln(2)}}}+\dfrac{1}{3^{x-\frac{\ln(x)}{\ln(2)}}}+\cdots+0>xN-x+1>N$ for all $x\in \left]1,1+\delta\right[$
I substitue $y = x-\frac{\ln(x)}{\ln(2)}$ and get:
$1+\dfrac{1}{2^{y}}+\dfrac{1}{3^{y}}+\cdots+0>xN-x+1>N$
This is true for all $y\in \left]1,1+\delta_{1}\right[$ where $\delta_{1}>0$ It is true, because:
for $1+\delta>x>1$ I can get $2x-2>\ln(x) \Leftrightarrow x-1>\dfrac{\ln(x)}{2} \implies y=x-\dfrac{\ln(x)}{2}>1$ and because $x$ is limited by $1+\delta$ I can find a new smaller $\delta_{2}>0$ so
$1+\dfrac{1}{2^{y}}+\dfrac{1}{3^{y}}+\cdots+0>xN-x+1>N$ is true for all $y\in \left]1,1+\delta_{2}\right[$
Finally
Now I'm done. If I choose a $N\in \mathbb{R}$ I can go iteratively from 1.25 to a value above $N$.
My question
My question is very simple. I know it's long (and "ugly"), but does it looks right? The strategy is "homemade", so I'm a bit insecure.
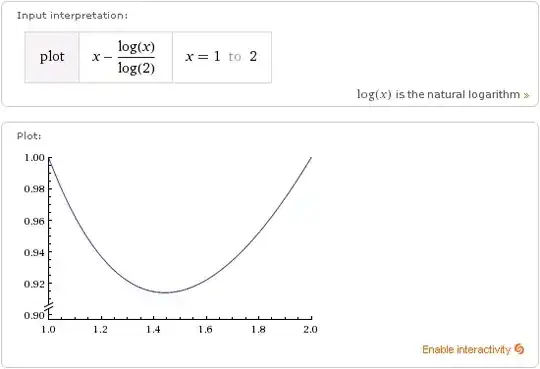
I know claim that if the statement is true for N=1.25, I can then deduce that it is true for a value xN-x+1>N and therefore iterate.
– bemyguest May 12 '12 at 22:21