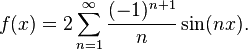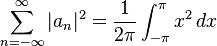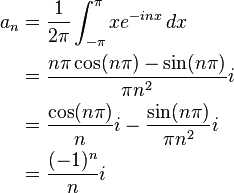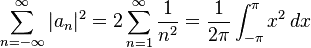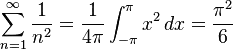0

How to find $1+1/2^2+1/3^2+...$ using Fourier Series. I have already worked out that the Fourier cosine series for $f(x) = x$ is:

$x = \frac{4L}{\pi^2} (1+\frac{1}{3^2}+\frac{1}{5^2} \cdots) -\frac{4L}{\pi^2}(\cos{\frac{\pi x}{L}}+...+\frac{1}{n^2}\cos{n \pi x/L}+...)$ where n is odd.

hint given is to evaluate this expression at $x = 0$. But then I just get $0 = 0$?

Edit, I have already worked out $1+1/3^2+1/5^2+... = \pi^2/8$

continental
  • 433
  • Try adding $1/2^2 + 1/4^2 + 1/6^2 + \ldots = 1/2^2(1 + 1/2^2 + 1/3^2 + \ldots)$ on both sides of your final equation and solve for the sum $S=1+1/2^2+1/3^2+\ldots$. – Winther Sep 15 '15 at 22:21
  • Is there anyway to specifically use the hint? – continental Sep 15 '15 at 22:21
  • @dable Probably you would be more likely to get the sort of answer you want if you include more of the original problem as stated. Aleksandar's answer answers the question as written but your edit and comment suggest this isn't what you're actually looking for. – Travis Willse Sep 15 '15 at 22:28
  • 1
    Related: http://math.stackexchange.com/questions/8337/different-methods-to-compute-sum-limits-k-1-infty-frac1k2 – Travis Willse Sep 15 '15 at 22:28

2 Answers2

3

Let $f(x)=x$ over the interval $x \in (-\pi,\pi)$. The Fourier series of this function is

enter image description here

Using Parseval's identity we obtain,

enter image description here

Where

enter image description here

Thus, $|a_n|^2=\frac{1}{n^2}$.

enter image description here

and,

enter image description here

Q.E.D

Aleksandar
  • 1,771
1

If you proved $$ \sum_{k\geq 0}\frac{1}{(2k+1)^2}=\frac{\pi^2}{8},$$ the remaining part is easy. Just notice that: $$ \zeta(2)=\sum_{n\geq 1}\frac{1}{n^2}=\sum_{k\geq 0}\frac{1}{(2k+1)^2}+\sum_{k\geq 1}\frac{1}{(2k)^2} = \frac{\pi^2}{8}+\frac{\zeta(2)}{4},$$ hence $\frac{3}{4}\zeta(2)=\frac{\pi^2}{8}$ gives: $$ \zeta(2)=\frac{\pi^2}{6}$$ as wanted.

Jack D'Aurizio
  • 353,855