3

I want to prove that every open interval has the same cardinality of R.

I've proved that $|(a,b)|=|(c,d)|$ so I may find a bijection $f: (a,b) \to (c,d)$.

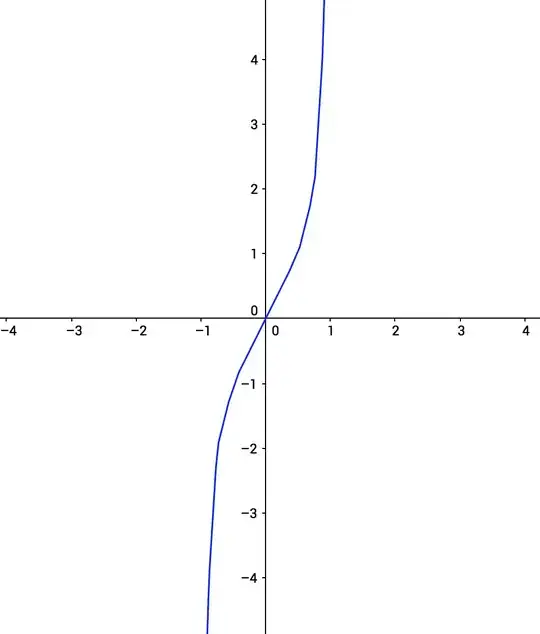
I need a bijection $f: (c,d) \to \Bbb R$ (a bijection defined by an interval to $\Bbb R$) The problem is that the only function like this that I know is tan(x) that is bijective in ($- \pi/2, \pi/2)$ but I am not allowed to use trigonometric functions.

Does anybody know another function like this?

Martin Sleziak
  • 53,687
Alex Turner
  • 754

2 Answers2

4

Are you allowed to use fractions? In that case, you could use $$ \frac{1}{c-x} + \frac{1}{d-x} $$ Of course, you would have to do some work to prove that it is monotonous on $(c, d)$, but that shouldn't be too hard (you are allowed to use differentiation, are you not?)

Arthur
  • 199,419
  • No, I am not allowed to use differentiation. I could not prove that it is surjective. – Alex Turner Sep 15 '15 at 22:09
  • If you are not allowed to use any analysis, use algebra precalculus: given $y\in\Bbb R$, solve for $x\in(c,d)$ the equation $\frac1{c-x} + \frac1{d-x}=y$. There is a quadratic equation underneath, and the solution is $x=\frac{c+d}2-\frac1y+\frac y{|y|}\sqrt{\frac1{y^2}+\frac{(d-c)^2}4}$ if $y\ne0$. (If $y=0$, the solution is much simpler.) – Anne Bauval Mar 05 '24 at 17:49
2

You already know that there is a bijection $(c,d) \to (-1,1)$ and it thus suffices to find a bijection $f \colon (-1,1) \to \mathbb R$. The following will do:

For all $n \in \mathbb N_0$ we let $f \restriction_{[1- 2^{-n},1-2^{-n-1}]}$ be the linear function from $(1- 2^{-n} ; 2^n)$ to $(1-2^{-n-1} ; 2^{n+1})$ and likewise $f \restriction_{[-1+ 2^{-n-1},-1+2^{-n}]}$ is the linear function from $(-1+ 2^{-n-1} ; -2^{n+1})$ to $(-1+ 2^{-n} ; -2^{n})$.

The picture below demonstrates what's going on:

enter image description here

Stefan Mesken
  • 16,651