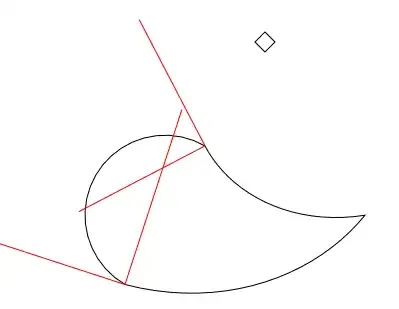
I have had success developing teardrop (or paisley) shapes with the Joukowsky (or Joukowski) transform. The transform is described in detail in Wikipedia's Joukowsky transform article. In a nutshell, it is a conformal mapping of a circle in the complex plane to a curved, cusped shape. Historically, it has been used in the development of airfoils. However, it lends itself nicely to the paisley problem. There are three parameters that allow you to adjust the length, width, and curvature of the teardrop.
My simplified three-parameter version of the transform is shown here:
Parameters: $C, m, \delta$
$\zeta_1 = m e^{i\delta}$
a = $|\zeta_1-C|$
$\zeta = \zeta_1 +a e^{i\theta}; \theta = [0,2\pi]$
$z = \zeta + C^2/\zeta$
You can see that $\zeta$ is a circle of radius $a$, centered at $\zeta_1$ that passes through the point $C$ on the real axis. $m$ is distance from the origin to $\zeta_1$. $z$ is the transformed circle, i.e., the teardrop.
Bearing in mind that this is not a simple problem, the parameter $C$ primarily controls the length of the teardrop, parameter $m$ the width, and $\delta$ the curvature (this angle should be in the $2^{nd}$ quadrant). A good parameter set to start experimenting with is $[C, m, \delta] = [1, 1/2, 2\pi/3]$. (NOTE: if $\delta$ is in the $3^{rd}$ quadrant the teardrop will 'bend' in the opposite direction; for example $\delta = 4\pi/3$ gives the conjugate of $\delta = 2\pi/3$.)
I've had some further thoughts on paisley shapes. Basically, you can take any yin-yang construct and use only half of it. In reality, take any antisymmetric spiral (think Cornu or Fermat, for example) and run a connecting semicircle or ellipse connecting the ends. You can get pretty fancy by allowing the spirals to curl up as well, if that suits your needs. Here's an example of such a yin-yang construct with a $6^{th}$-order polynomial spiral. I have developed all manner of yin-yang constructs with various functions, some of which can be found here: http://web.calstatela.edu/curvebank/waldman5/waldman5.htm.