I am asked to find $2^{1/5} $. Using the formula, and noticing $2 = 2e^{0 i} $, we have
$$ 2^{1/5} = 2^{1/5} \bigg( \cos( \frac{ 0}{5} + \frac{ 2 \pi k}{5} ) + i \sin( \frac{ 0}{n} + \frac{ 2 \pi k}{n} ) \bigg) $$
My confusing. I notice we can also write $2 = 2e^{2 \pi k} = 2e^{4 \pi k} = .... $ Do I need to consider every case, or would it be enough to just consider the case when $2 = 2e^{0i } $ as above?
One way to attack this baby is to remember that the number of $n$-th complex roots of a number is always $n$, and that those $n$ roots form the vertices of an $n$-sided regular polygon on the Complex plane. So there are $3$ cube roots, forming a triangle, $4$ cube roots, forming a square, $5$ fifth roots, forming a pentagon, and so forth.
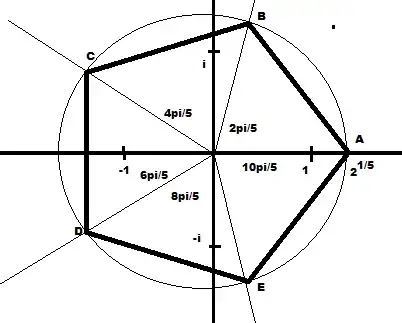
Int the above diagram, the pentagon is superimposed on the Complex plane. It has been broken broken up into five segments. The angle between each segment is $1/5$ that of a full circle. That is, each angle is $2\pi/5$. Each of the points, $A$ to $E$ is located by two numbers: One number is the distance from the centre of the figure. The other number is the angle that around the circle that it's located away from point $A$.
The angles are marked on the diagram. $A$ is $0$, (but it's marked on the diagram as $10\pi/5=2\pi$ because travelling $2\pi$ radians from any point on a circle will take you back to where you started).
Your angles are as follows:
$A. 0$
$B. 4\pi/5$
$C. 2\pi/5$
$D. 6\pi/5$
$E. 8\pi/5$
The number you also want to know the argument which is the Real number value of the length of each of those spikes from the centre to a point. That number is the Real value of $2^{1/5}$.
How do you arrange all this information is your final stretch. If we designate $z$ as your Complex root, $r$ as your argument (which is $2^{1/5}$ in each case) and $\theta$ for your angles, your general forms are:
$$z = r(\cos\theta + i\sin\theta)$$ and $$z = e^{i\theta}$$
(Why these are equivalent is another story.)
So, your five roots are:
$$A.\; 2^{\frac{1}{5}}e^{0i}=2^{\frac{1}{5}}$$ $$B.\; 2^{\frac{1}{5}}e^{2\pi i/5}$$ $$C.\; 2^{\frac{1}{5}}e^{4\pi i/5}$$ $$D.\; 2^{\frac{1}{5}}e^{6\pi i/5}$$ $$E.\; 2^{\frac{1}{5}}e^{8\pi i/5}$$
Alternatively, these can be expressed as:
$$A.\; 2^{\frac{1}{5}}(\cos 0 + i\sin 0)= 2^{\frac{1}{5}}$$ $$B.\; 2^{\frac{1}{5}}(\cos \frac{2\pi}{5} + i\sin \frac{2\pi}{5})$$ $$C.\; 2^{\frac{1}{5}}(\cos \frac{4\pi}{5} + i\sin \frac{4\pi}{5})$$ $$D.\; 2^{\frac{1}{5}}(\cos \frac{6\pi}{5} + i\sin \frac{6\pi}{5})$$ $$E.\; 2^{\frac{1}{5}}(\cos \frac{8\pi}{5} + i\sin \frac{8\pi}{5})$$
These are your five roots, each expressed in two forms. The first form is polar and the second is rectangular.
Any of these numbers, multiplied by itself five times will yield $2$. Multiplying a rectangular form by itself five times is tedious. Multiplying a polar form is amazingly simple. I'll end off with one example.
$$[2^{\frac{1}{5}}e^{4\pi i/5}]^5=[2^{1/5}]^5[e^{4\pi i/5}]^5= 2e^{20\pi i/5}=2e^{4\pi i}$$
Since $4\pi$ is two full rotations about the circle, $e^{4\pi i}=e^{0 i}=1$
So the equation above finishes:
$$2e^{4\pi i}= 2(1) = 2$$
which is what we wanted to show.
EDIT:
To address the OP directly, you can always add $2\pi$ to any angle without changing the value of $z$ just as you can go around a circle exactly once and end up where you started.
So, you need only show the solution for $\theta=0$ and $\theta=2\pi$ takes care of itself.
Hint: Put $2=x^5$;$x^5=1.2$ Now take 5th roots of both sides. And then use all $5$ 5th roots of unity.
