Achilles and the tortoise paradox?

Question

Let's say we decide to race on a track $1000$ km long. You are a $100$ times faster than me, meaning if we both start at the beginning, you obviously win. To make things more fair you give me a head start of $1$m. The distance is still very small, meaning you will obviously win.

A few premises:

-For you to win the race you need to overtake me

-To overtake me you need to reach a point of equivalence

-If there is no point of equivalence you can't beat me

Let's assume it takes you $1$ second to reach 1m. However in that $1$ second, I would have travelled a distance forward-lets say I am now at $1.01$m. You haven't caught up to me- I'm still $0.01$m ahead of you. It takes you $0.01$s to travel that $0.01$m. But in that $0.01$ s I would have travelled $0.0001$m, meaning I'm still ahead of you. Therefore you can never catch up to me- the distance between us will get infinitesimally small, but never $0$. Therefore since you can't catch up to me, you can never win.

This obvious paradox has been resolved through the fact that an infinitesimal series adds up to one- however, doesn't thid simply prove both people will finish the race? How does it prove the faster person will win?

Please don't simply give me a linear solution. I do not want to know when the faster person catches up - I want to know the mathematical flaw in the paradox's logic.

Answer 1

If you start 1 meter ahead of me, and it takes me 1s to reach your current position (apparently I run at 1 meter per second, and you run at .01 meters per second), $\frac{1}{100}$th of a second to reach your position at $t=1$, etc. I take $$1 + \frac{1}{100}+\frac{1}{100^2} + \cdots = \sum_{i=0}^{\infty}\frac{1}{100^i}$$ seconds to overtake you. Since $$\sum_{i=0}^{\infty}\frac{1}{100^i} = \frac{1}{1-\frac{1}{100}} = \frac{100}{99},$$ then after $\frac{100}{99}$ seconds, I will have overtaken you. This will occur well before we reach the finish line; we've only advanced $\frac{100}{99}$ meters (since apparently I run at 1 meter per second), and the finish line is more than $\frac{100}{99}$ meters from where we started. After I've overtaken you, I will be ahead at any further time.

The implicit error in the original claim that I cannot overtake you is the assumption that an infinite sum of positive quantities will necessarily be infinite. This has long been dealt with, and does not even require the use of infinitesimals.

Of course, it's possible for you to start so far ahead of me that I will only catch up to you when we get to the finish line; but that's hardly a paradox! Nor do I understand what your complaint is with "both people finish the race". Is there some problem with the slower person finishing after the faster one has?

Answer 2

Below are some pointers to the literature for your philosophical concerns, taken from old sci.math posts of mine. Thus, this is really in the nature of a comment, not an answer, but because of comment length constraints I'm posting this as an answer.

First, of possible interest are the google searches infinity machines and supertasks, as well as the Wikipedia article Supertask.

I've listed the references that follow in order of how helpful/interesting I think they'd be for your concerns.

[1] Wesley Charles Salmon (editor), Zeno's Paradoxes, Bobbs-Merrill, 1970, x + 309 pages. [Reprinted by Hackett Publishing Company in 2001; ?? + 320 pages.]

[2] José Amado Benardete, Infinity. An Essay in Metaphysics, Clarendon Press, 1964, x + 289 pages. scanned copy

[3] Adolf Grünbaum, Modern Science and Zeno's Paradoxes, Wesleyan University Press, 1967, x + 148 pages. [Reprinted by George Allen and Unwin in 1968; x + 153 pages.]

[4] Florian Cajori, The history of Zeno's arguments on motion (in 9 parts), American Mathematical Monthly 22 (1915), 1-6, 39-47, 77-82, 109-115, 143-149, 179-186, 215-220, 253-258, 292-297. Jstor AMM Volume 22 issues: 1 2 3 4 5 6 7 8 9

[5] Florian Cajori, The purpose of Zeno's arguments on motion, Isis 3 #1 (January 1920), 7-20. jstor

[6] Clive William Kilmister, Zeno, Aristotle, Weyl and Shuard: two-and-a-half millenia of worries over number, Mathematical Gazette 64 #429 (October 1980), 149-158. jstor

Answer 3

I think the mathematical "explanation" of the Zeno's paradox (convergence of infinite series) is quite unsatisfying. Assuming that each term in the series corresponds to one step of Achilles's and considering that he indeed overtakes the turtle in finite time, which of Achilles feet is forward at the moment when he reaches the turtle?

Or a slightly different, but equivalent, presentation of the paradox: assume that the turtle changes direction at each discrete instant of time Achilles reaches her previous position, alternatively moving NE and SE. Achilles just follows her path. What direction is the turtle facing the moment Achilles reaches her?

Achilles's and the turtle is no paradox at all, but a refutation of the hypotheses that the space is continuous. Zeno's arrow paradox is a refutation of the hypothesis that the space is discrete. Together they form a paradox and an explanation is probably not easy. For Zeno the explanation was that what we perceive as motion is an illusion. In any case, I don't think that convergent infinite series have anything to do with the heart of Zeno's paradoxes.

EDIT: The same argument can be made point-like particles, only assuming that physical reality is continuous and infinitely divisible. Imagine a photon travelling between an infinite sequence of mirrors placed in a zig-zag shape with distance between mirrors decreasing at a geometric rate. So the photon bounces from a NE to SE direction and back, with the distance travelled decreasing "fast". Since the length of the total path is finite (sum of a geometric series), the photon will emerge from the sequence of mirrors in finite time. What direction will it travel? The heart of the Zeno's argument is that there is no logical way to decide that. You may argue that it is impossible to build such a sequence of mirrors, however this is just conceding Zeno's point that physical reality is NOT continuous and infinitely divisible.

I think the mathematical model of the Zeno's paradox is a great pedagogical tool in first year calculus, probably could be made even earlier in high school, but it misses an important aspect of Zeno's argument. Granted, this argument lies at the boundary of math, physics and perhaps philosophy.

Answer 4

Another way to look at it without calculus or infinitesimals: Between any two distinct points A and B on a line L, there are infinitely many other points. An object going from A to B along L, will pass through each one of these points in a finite length of time. What may seem paradoxical about this scenario is that an infinite number events (the arrival at each point) will happen in a finite length of time. But there is nothing really paradoxical about it. If the object in question maintains a constant speed $s$ (as both the tortoise and Achilles are assumed to do in your example), you can calculate its distance traveled $d$ after any given time $t$ using a simple formula ($d=st$).

Now calculate the position of both the tortoise and Achilles at $\frac{1}{99}$ seconds after Achilles sets out. They will be at the same point at this time.

For the sake of completeness, here is the "linear solution:"

Achilles (the faster runner): $d_A=100t$

Tortoise (the slower runner): $d_T=1+t$

where $t=0$ when Achilles sets out.

When is $d_A=d_T$? When $t=\frac{1}{99}$ seconds.

Answer 5

Short answer: When two procedures used to solve a problem lead to different results (a paradox), the solution to the paradox is to show why one of the procedures is wrong. It is NOT showing why the wrong procedure must, would, or should lead to the same result. A complete explanation, and the solution, are given below.

What Does Solving a Paradox Mean?

As mentioned at the beginning of my article (at: https://bit.ly/2IM76rF ), a paradox proposes the existence of two different results as a solutions for the same problem. These results are inconsistent with each other, depending on which procedure is used. Only one can be correct. As Brown and Moorcroft suggest, we are not looking for a mathematical demonstration that Achilles reaches the tortoise. Assuming they are both running in the same direction, we know he will. We can calculate the exact time, given the distance between the two and the two speeds, using a simple formula:

t = distance/(difference in velocity)

Instead, explaining or invalidating a paradox is to show a fault in the paradox formulation, or the proposed solving procedure, so that we can exclude this procedure and demonstrate that there is only one result for the original problem. The solution of a paradox is the answer to the question: “How does the paradox formulation misrepresent reality or logic?” That is, we need to show why the proposed method is conceptually wrong. Solving a paradox, invalidates the formulation of a problem proposed by the author of the paradox and leaves us with only valid procedures for solving the original problem.

Why were the previous proposed solutions for the paradox not satisfactory?

Most, if not all, the proposed solutions to Zeno’s paradox assume that Zeno’s proposed procedure is correct. The procedure seems to be logical when it is first introduced to us, but we will see that the procedure proposed by Zeno is conceptually incorrect. The authors then used a procedure similar to Zeno’s faulty procedure to reach the expected correct result for the original problem.

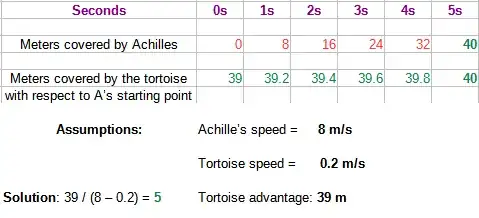
For example, the simple way mentioned earlier to solve the problem (not the paradox) can be examined using a spreadsheet. Given the assumptions in the diagram below, the time for Achilles to reach the tortoise is 5 seconds:

39 m / 7.8 m/s = 5 s

If we calculate a sum of an infinite series, as several mathematicians have suggested, we obtain the same result: Achilles will reach the tortoise. By applying any legitimate mathematical solution to the problem, we state, in another way that: We can prove that Achilles reaches the tortoise.

What is the problem then?

We know that Zeno is wrong: The fact that his procedure never ends, does not imply that Achilles will never reach the tortoise. We can prove this mathematically in many ways. Intuitively we all agree with the mathematicians. However, when mentally following the proposed repetitive procedure, the paradox puzzles our mind.

What are the facts?

1. Asserting that Zeno’s procedure never ends is correct, as we can prove it by writing a recursive computer program that follows Zeno’s steps. The program will never end, and never will provide us with the expected result, because the condition for the end of the recursion process (Achilles reaches the tortoise) would never occur.
2. Asserting that Achilles never reaches the tortoise is wrong, as we can prove that he does, by using several mathematical procedures.

Thus, we must conclude that Zeno’s procedure to solve the problem, is not correct.

The question then is: Why is Zeno’s procedure wrong? The key word in the previous assertions is “never”. Never implies time and the problem must be considered in the context of space and time.

The Explanation of Zeno's Paradox:

Zeno's proposition invites the solver to do a series of steps each time changing system of reference: STEP 1: The starting system of reference: The point where Achilles starts the race and the tortoise is well ahead, STEP 2: After a while, we are then asked to use a new system of reference: The point where Achilles reached and where the tortoise initially started, with the the tortoise now a bit further ahead, STEP 3: Then again we are asked to use, recursively, a new system of reference with the new starting point for Achilles and with the tortoise still further ahead, with every step we are asked to freeze the process and then continue by re-creating and examining the original problem using a different system of reference.

Today we know more about the relative motion of two bodies. Solving a problem that involves space and time, requires a defined system of reference, which cannot be changed without the proper conversions.

NOTE: The concept of a system or reference, or frame of reference, in elementary physics is founded on Einstein's Special Theory of Relativity, First Postulate: All velocities are measured relative to some frame of reference.

After Zeno's proposed first step, or first change of system of reference, the problem, as presented in the second step, is exactly the same as the original, the only change being a difference in "scale". No progress was achieved in solving the problem. Changing system of reference essentially restarts the problem-solving procedure. This realization implies that the problem is never going to reach a conclusion as the step by step procedure is reiterated. If the system of reference is changed at every step, our working spacetime shrinks with every step, the solution becomes elusive and the tortoise becomes apparently unreachable. Zeno proposes a procedure that never ends, for solving a problem that has a trivial solution.

Our Solution (Why is Zeno's Formulation Incorrect)

Our solution of Zeno's paradox can be summarized by the following statement:

"Zeno proposes observing the race only up to a certain point, using a system of reference, and then he asks us to stop and restart observing the race using a different system of reference. This implies that the problem is now equivalent to the original and necessarily implies that the proposed procedure for solving the problem will never end."

That is, we cannot change system of reference in the middle of a problem involving velocity, space and time, whether the frame of reference is openly stated, or implied.

As an analogy, you cannot solve a problem involving measurements by using English Imperial measures at the start of calculations and then switch to metric measures (without proper conversions) in the middle of calculations.

Zeno's trick works, and puzzles our mind, because we are used to assume one frame of reference when solving this type of problems.

An example

The following is not a “solution” of the paradox, but an example showing the difference it makes, when we solve the problem without changing the system of reference. In this example, the problem is formulated as closely as possible to Zeno’s formulation.

Zeno would agree that Achilles makes longer steps than the tortoise. Let’s assume that one Achilles-step is about 20 tortoise-steps long, and let’s also assume that both Achilles and the tortoise make the same number of steps in the same amount of time. For example, two steps per second (the exact amount doesn’t really matter). If the tortoise starts the race 20 Achilles-steps ahead of him, then after 20 steps Achilles reaches where the tortoise was (See diagram below: Tortoise starting point).

In the meantime, the tortoise has made 20 of her steps, and she is now one full Achilles-step ahead of him. We have not changed our system of reference. We referred to both starting points. These did not move relatively to each other. We could choose any fixed ground point. To please Zeno, let’s continue by referring to the tortoise starting point, where Achilles currently is. When both runners make one more step, step 21, the tortoise will have moved by one of her steps and she will still be ahead of Achilles by that one tortoise-step. Achilles is now one Achilles-step ahead of the tortoise starting point. Now, let’s continue, without changing the system of reference. This is the key point. We do not redefine the problem and use the current positions of the runners as new starting points, as Zeno proposes, but we refer to the information about the race we have already accumulated in our knowledge base. Achilles then completes his 22nd step, and he is two Achilles-steps ahead of the tortoise starting point. The tortoise will have completed her 22nd tortoise-step from her starting point. Hence the tortoise is now behind Achilles by 18 tortoise-steps. Thus, if we do not change the system of reference, the paradox does not appear.

Answer 6

The Paradox for Achilles and the Tortoise

Zeno’s “paradox” is that the swift Achilles cannot catch the plodding tortoise. In this paradox Zeno bases his argument on Dichotomy.

A dichotomy is any splitting of a whole into two non-overlapping parts, meaning it is a procedure in which a whole is divided into two parts. It is a partition of a whole (or a set) into two parts. The 2 parts are then treated seperately. In above example, the movement of Achilles and the tortoise are treated independent from each other and consequentlt Achilles will never catch the tortoise.

To put Zeno’s paradox into math, let the speed of Achilles A be denoted by VA and that of the tortoise T by VT.

The time of movement t for both is the same. At the start, there is a distance DO between them. Let’s look at some of the intervals.

DO = VA x t D1 = VT x t

Since t is the same, substitute t = DO / VA into D1 which yields D1 = VT x DO / VA Now Achilles has to cover the distance D1 needing time t = D1 / VA But the tortoise, in the meantime goes ahead D2 = VT x D1 / VA. Now Achilles has to cover the distance D2 needing time t = D2 / VA But the tortoise, in the meantime goes ahead D3 = VT x D2 / VA. As can be seen this is a recursive equation

Di+1 = VT x Di / VA where i = 0, 1, 2, 3, …..infinity. The distances getting smaller and smaller but A will never catch T

Now let’s solve the problem using physics. Achilles and the tortoise will meet at time t. Achilles needs to run the distance DO plus the distance the tortoise moved in the meantime. Thus, the time needed is t = (DO + DT}/VA The tortoise, in the same time covers t = DT / VT Equating the 2 equations leads to

(DO + DT}/VA = DT / VT

Solving for the unknown distance DT the tortoise has to run before being caught yields DT = (DO x VT)/( VA - VT)

Achilles has to run DA = DO + DT

The time needed for intersection is T = ( DO/ VA) x [1 + VT/( VA - VT)]

Verification: If VA = VT then DT approaches infinity that means they never meet. If VT = 0 then they meet at the initial distance DO

Test example DO = 10m, VA = 2m/s, VT = 1m/s Results: DT = 10m, DO = 20m, t = 10s