6

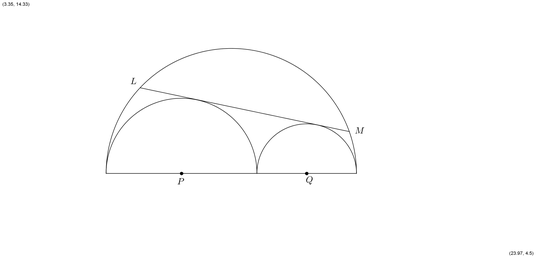
In the diagram,the semicircles centered at ${P}$ and $Q$ are tangent to each other and to the large semicircle ,and their radii are $6$ and $4$ respectively.Line $LM $ is tangent to semicircles $P$ and $Q$ .Find $LM$ enter image description here

Efforts made: I've been able to calculate the length of the segment between the points of tangency of the interior semicircles ,but i've not been able to find the lengths of the external segments.

This problem is meant to be solved by synthetic methods(geometric methods). thanks in advance

Nameless
  • 1,480
  • What is the difference between the "tangent common to both interior semicircles" and the line segment LM? – uniquesolution Sep 10 '15 at 09:33
  • What do you mean ? – Nameless Sep 10 '15 at 09:37
  • I mean, the problem asks to find LM, and you say that you calculated the length of the segment tangent to both interior semicircles, which as far as I can see, is exactly LM, so I asked you what is the difference. It was not a hint, but a genuine question. – uniquesolution Sep 10 '15 at 09:40
  • 1
    @uniquesolution: LM touches the two semicircles in two points, let's call them A and B, respectively. The length of the segment AB determined by those two points of intersection has already been calculated by the OP. What's missing is the remaining two segments, LA and MB. – Lucian Sep 10 '15 at 09:46
  • Ah ,yes sorry i see my wording isn't really techinical.However i was trying to say that i calculated the segment which is between the points of tangency of the interior semicircles.Forgive me – Nameless Sep 10 '15 at 09:46
  • ok thanks. one way is to choose a coordinate system so that the point $Q$ is the origin, so the equations of the three circles are known and so the equation of the common tangent can also be found. – uniquesolution Sep 10 '15 at 09:52
  • What do you mean by "synthetic methods"? – uniquesolution Sep 10 '15 at 09:56
  • No analytical methods allowed – Nameless Sep 10 '15 at 09:58
  • Did you get $\sqrt96$ for the length of the segment between points of tangency? I'm trying to see if I'm in the right track.. – ChrisJWelly Sep 10 '15 at 10:13
  • yes i got the same – Nameless Sep 10 '15 at 10:16
  • I had used the assumption that the line P to the point of tangency of the larger semicircle is parallel to the line Q to the point of the tangency of the smaller semicircle. Do you happen to know why this is true? – ChrisJWelly Sep 10 '15 at 11:47
  • i think you have to consider the trapezoid formed by the centers of the semicircles and the points of tangency (if i am undersatnding correctly what you're asking) – Nameless Sep 10 '15 at 11:57

2 Answers2

1

DISCALIMER : This is a brute force method using coordinate geometry. A better method should exists.

Take the center of the large circle be $(0, 0)$. Then $P = (-4, 0)$ and $Q = (6, 0)$.

Now let $y = mx + c$ denote the line extending $LM$ on both sides, where $m, c \in \mathbb{R}$ are constants such that both the systems of equations,

$$y = mx + c$$ $$(x - (-4))^2 + y^2 = 6^2$$

and

$$y = mx + c$$ $$(x - 6)^2 + y^2 = 4^2$$

have only one unique solution.

From the first system we can work out, by substitution first and then by considering discriminant second, one required condition:

$$(2mc + 8)^2 - 4(m^2 + 1)(c^2 - 20) = 0$$ $$20 m^2 + 8mc - c^2 + 36 = 0$$

and similarly from the second system,

$$(2mc - 12)^2 - 4(m^2 + 1)(c^2 + 20) = 0$$ $$20m^2 + 12mc + c^2 - 16 = 0$$

Subtract the twice the second condition from thrice the first to eliminate $mc$:

$$3(20 m^2 + 8mc - c^2 + 36) - 2(20m^2 + 12mc + c^2 - 16)= 0$$ $$20m^2 -5c^2 + 140 = 0$$ $$c^2 = 4m^2 + 28$$

Now consider the sum of $4$ times the first condition and $9$ times the second condition to eliminate the constant term:

$$4(20 m^2 + 8mc - c^2 + 36) + 9(20m^2 + 12mc + c^2 - 16) = 0$$ $$52m^2 + 28mc + c^2 = 0$$ $$(2m + c)(26m + c)$$

From which we get either $c = -2m$ or $c = -26m$.

Using the results in the previous two parts, we see that there a few possibilities for $m$. Clearly $c = -2m$ has no solutions because

$$(-2m)^2 = 4m^2 + 28$$

has no solution for $m$. Hence $c = -26m$. Therefore

$$(-26m)^2 = 4m^2 + 28$$ $$672m^2 = 28$$ $$m = \pm \frac{1}{2\sqrt{6}}$$

Since from our geometric definition of $m$ being the gradient of the negatively sloped $LM$-extended, $m$ must be negative. Hence

$$m = -\frac{1}{2\sqrt{6}}$$

which leaves $$c = \frac{13}{\sqrt{6}}$$

Thus, the line $LM$ extended has equation $y = -\frac{1}{2\sqrt{6}}x + \frac{13}{\sqrt{6}}$

Now use the equation of $LM$ extended and the equation of the large circle (with radius $\frac{6 + 6 + 4 + 4}{2} = 10$,

$$x^2 + y^2 = 10^2$$

to find the coordinates of $L$ and $M$.

Finding the distance between $L$ and $M$ then becomes trivial (Pythagoras' Theorem).

Yiyuan Lee
  • 14,435
1

Let $A$ and $B$ be the tangency points of semicircles $P$ and $Q$ respectively, and let $O$ be the centre of the large semicircle (with radius 10). Then let $R$ be the tangency point of semicircle $Q$ to $O$.

Extend $LM$ and $QR$ to intersect at $T$. Since $\triangle ATP\sim \triangle BTQ, \frac{RT+4}{4}=\frac{RT+14}{6}\implies RT=16.$

Now let $S$ be on $LT$ such that $OS||QB$. Then $\frac{QT}{OT}=\frac{QB}{OS}$, so $\frac{20}{26}=\frac{4}{OS}$ , hence $OS=\frac{26}{5}$.

Since $OL=OM=10$, we can now directly compute the answer using the Pythagorean theorem