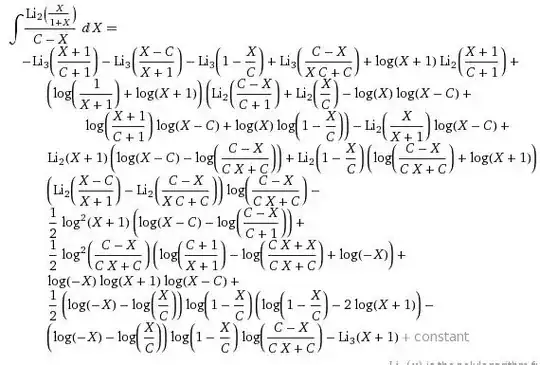3

For $a,c\in\mathbb{R}\land-1\le a\land-1<c$, define the function $J{\left(a,c\right)}$ to be the value of the dilogarithmic integral

$$J{\left(a,c\right)}:=\int_{0}^{1}\mathrm{d}y\,\frac{\operatorname{Li}_{2}{\left(\frac{c}{1+c}\right)}-\operatorname{Li}_{2}{\left(\frac{ay}{1+ay}\right)}}{c-ay}.$$

In principle, $J{\left(a,c\right)}$ may be evaluated in terms of trilogs, dilogs, and elementary functions. In the process of trying to develop my own solution, I managed to obtain partial solutions valid over various subsets of the parameter space $(a,c)\in[-1,\infty)\times(-1,\infty)$, but I would prefer an alternative approach that eliminates the need for all the casework and produces a single expression valid over all parameter choices (excepting possibly at $a,c=-1,0$). Any suggestion/hints are welcome. Cheers!

Progress so far:

Defining the auxiliary parameters $A:=1+a,~C:=1+c$, we find:

$$\begin{align} J{\left(a,c\right)} &=\int_{0}^{1}\mathrm{d}y\,\frac{\operatorname{Li}_{2}{\left(\frac{c}{1+c}\right)}-\operatorname{Li}_{2}{\left(\frac{ay}{1+ay}\right)}}{c-ay}\\ &=\int_{0}^{1}\mathrm{d}y\,\frac{1}{c-ay}\int_{ay}^{c}\mathrm{d}z\,\frac{\ln{\left(1+z\right)}}{z\left(1+z\right)}\\ &=\int_{0}^{1}\mathrm{d}y\,\frac{1}{c-ay}\int_{1+ay}^{1+c}\mathrm{d}x\,\frac{\ln{\left(x\right)}}{\left(x-1\right)x};~~~\small{\left[1+z=x\right]}\\ &=-\frac{1}{a}\int_{\frac{1}{1+c}}^{\frac{1+a}{1+c}}\mathrm{d}t\,\frac{1}{\left(1-t\right)}\int_{\left(1+c\right)t}^{1+c}\mathrm{d}x\,\frac{\ln{\left(x\right)}}{x\left(1-x\right)};~~~\small{\left[\frac{1+ay}{1+c}=t\right]}\\ &=-\frac{1}{a}\int_{\frac{1}{C}}^{\frac{A}{C}}\mathrm{d}t\,\frac{1}{\left(1-t\right)}\left[\int_{0}^{C}\mathrm{d}x\,\frac{\ln{\left(x\right)}}{x\left(1-x\right)}-\int_{0}^{Ct}\mathrm{d}x\,\frac{\ln{\left(x\right)}}{x\left(1-x\right)}\right]\\ &=-\frac{1}{a}\int_{\frac{1}{C}}^{\frac{A}{C}}\mathrm{d}t\,\frac{1}{\left(1-t\right)}\left[\int_{0}^{C}\mathrm{d}x\,\frac{\ln{\left(x\right)}}{x\left(1-x\right)}-\int_{0}^{C}\mathrm{d}w\,\frac{\ln{\left(tw\right)}}{w\left(1-tw\right)}\right];~~~\small{\left[x=tw\right]}\\ &=-\frac{1}{a}\int_{\frac{1}{C}}^{\frac{A}{C}}\mathrm{d}t\int_{0}^{C}\mathrm{d}x\,\left[\frac{\ln{\left(x\right)}}{\left(1-x\right)\left(1-tx\right)}-\frac{\ln{\left(t\right)}}{x\left(1-t\right)\left(1-tx\right)}\right]\\ &=-\frac{1}{a}\int_{0}^{C}\frac{\mathrm{d}x}{1-x}\int_{\frac{1}{C}}^{\frac{A}{C}}\mathrm{d}t\left[\frac{\ln{\left(xt\right)}}{1-xt}-\frac{\ln{\left(t\right)}}{x\left(1-t\right)}\right]\\ &=\small{-\frac{1}{a}\int_{0}^{C}\frac{\mathrm{d}x}{1-x}\left[\frac{\operatorname{Li}_{2}{\left(1-\frac{Ax}{C}\right)}-\operatorname{Li}_{2}{\left(1-\frac{x}{C}\right)}}{x}-\frac{\operatorname{Li}_{2}{\left(1-\frac{A}{C}\right)}-\operatorname{Li}_{2}{\left(1-\frac{1}{C}\right)}}{x}\right]}\\ &=\small{-\frac{1}{a}\int_{0}^{1}\mathrm{d}y\,\frac{\operatorname{Li}_{2}{\left(1-Ay\right)}-\operatorname{Li}_{2}{\left(1-y\right)}-\operatorname{Li}_{2}{\left(1-\frac{A}{C}\right)}+\operatorname{Li}_{2}{\left(1-\frac{1}{C}\right)}}{y\left(1-Cy\right)}};~~~\small{\left[x=Cy\right]}\\ &=...\\ \end{align}$$

This feels like progress of a sort, but how best to proceed from there?

David H
  • 29,921
  • Just a question: What method do you use to get partial answers? Do you perhaps write the difference of dilogarithms as an integral $\int_{ay}^c \frac{\log(1+x)}{x+x^2},dx$ and change order of integration? If not, maybe it gives something (even though I cannot see how to avoid dividing into different cases when switching order of integration)... – mickep Sep 10 '15 at 10:36
  • @mickep Actually I obtained my partial answers the old-fashion way through integration by parts, which requires that you divide into cases from the get-go. However, I did try the method you describe next, but I ran into more problems. – David H Sep 10 '15 at 11:08

1 Answers1

1

$$J{\left(a,c\right)}=\int_{0}^{1}\mathrm{d}y\,\frac{\operatorname{Li}_{2}{\left(\frac{c}{1+c}\right)}-\operatorname{Li}_{2}{\left(\frac{ay}{1+ay}\right)}}{c-ay}$$

$$J{\left(a,c\right)}=\operatorname{Li}_{2}{\left(\frac{c}{1+c}\right)}\int_{0}^{1}\frac{\mathrm{d}y}{c-ay}-\int_{0}^{1}\mathrm{d}y\,\frac{\operatorname{Li}_{2} \left(\frac{ay}{1+ay}\right)}{c-ay}$$

$$J{\left(a,c\right)}=\operatorname{Li}_{2}{\left(\frac{c}{1+c}\right)} \left(\frac{-1}{a} \ln \frac{a-c}{c} \right) -\int_{0}^{1}\mathrm{d}y\,\frac{\operatorname{Li}_{2} \left(\frac{ay}{1+ay}\right)}{c-ay}$$ With change of variables : $X=ay$ and $C=c/a$ : $$\int_{0}^{1}\mathrm{d}y\,\frac{\operatorname{Li}_{2} \left(\frac{ay}{1+ay}\right)}{c-ay}= \frac{1}{a}\int_{0}^{1/a}\mathrm{d}X\,\frac{\operatorname{Li}_{2} \left(\frac{X}{1+X}\right)}{c-X}$$

For the last integral, WolframAlpha gives an huge result :

enter image description here

JJacquelin
  • 66,221
  • 3
  • 37
  • 87