For Bernoulli number $ B_n$, prove (or disprove) that the only integer solution for $\dfrac{B_{2m}}m= \dfrac{B_{2n}}n $ is $ (m,n) = (1,7) $ for $ 1\leq m <n $.
I have no clue how to prove this.
Thanks to Jack D'Aurizio, Barry Cipra, robjohn♦, whacka for helping out in the previous question.
Things that were mentioned:
1. Particular values of Riemann zeta function.
2. Von Staudt–Clausen theorem.
3. Euler–Maclaurin formula.
The Exponential Generating Function for the Bernoulli Numbers is $$ \frac{x}{e^x-1}=\sum_{n=0}^\infty B_n\frac{x^n}{n!} $$ Since this function has poles at $x=\pm\pi i$ we know that $$ \begin{align} \frac1\pi &=\limsup_{n\to\infty}\left(\frac{B_n}{n!}\right)^{1/n}\\ &=e\limsup_{n\to\infty}\frac{B_n^{1/n}}n \end{align} $$ Using deeper complex analysis, we have the Functional Equation for $\zeta(s)$: $$ \zeta(s)=2^s\pi^{s-1}\sin\left(\pi s\over2\right)\Gamma(1-s)\zeta(1-s) $$ Which says that $$ \frac{B_{2n}}{2n}=\zeta(-2n+1)=-\frac{2(2n-1)!}{(-4\pi^2)^n}\zeta(2n) $$ Now, we can actually compute $\zeta(2n)$ using the recursion in this answer, but what is important here is that it is very close to $1$ for large values of $n$.
Thus, for $n\ge\pi+1$, $\zeta(-2n+1)$ changes sign, but is growing in magnitude. Thus, once $\zeta(-2n+1)\ge\zeta(-1)$ (and as shown in this answer, that is at $n=7$), it will be greater than any previous value. Thus, for $n\gt7$, $\frac{B_{2n}}{2n}$ will be unique. Comparing the values for $n\le7$, we get that $$ \frac{B_{2n}}{2n}=\frac{B_{2m}}{2m} $$ for $1\le m\lt n$ only when $m=1$ and $n=7$.
Here is a plot of $\log\left|\frac{B_{2n}}{2n}\right|$
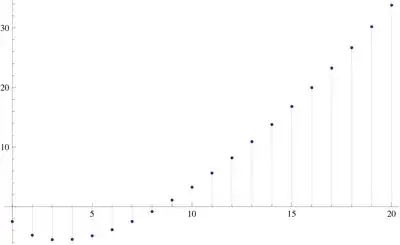
Note that for $n\ge4$, $\left|\frac{B_{2n}}{2n}\right|$ is monotonically increasing as described above, and that for $n\gt7$, $\left|\frac{B_{2n}}{2n}\right|$ is larger than any previous values.
