Is there any equation which describes or estimates the number of singular values of a Matrix $X$ ?
I found out that the number is equal to the number of eigenvalues of the Matrix $X^{*} X$, which are calculates as: $det( \lambda *I- X^{*} X)=0$. From these Eigenvalues I have to take the square roots and will get my singular values. But how do I see how many of those are equal to zero ?
- 61
- 1
- 7
2 Answers
That would be the rank of $X^*X$: the diagonalization of $X^*X$ is $$X^*X=P^{-1}DP$$ where $P$ is invertible, $D$ is diagonal with the eigenvalues on the diagonal.
- 15,854
-
That's right. Thanks! Is there any chance to determine the number of eigenvalues unequal to zero in $D$? – N8_Coder Sep 08 '15 at 08:10
-
Or what do you want to tell me with the diagonalization ? – N8_Coder Sep 08 '15 at 22:28
-
Just to show you that the number of non-zero singular values is equal to the rank of $X^X$. There are standard procedures to find the rank of $X^X$, e.g. Gauss elimination. – Quang Hoang Sep 09 '15 at 00:57
-
But why are you sure, that $X^*X$ can be diagonalized? That is not the general case. – N8_Coder Sep 09 '15 at 08:44
Matrix rank is a nuanced subject in numerical linear algebra because of errors in the finite binary representation of real numbers. In theory the matrix rank $\rho$ has a crisp definition. In computation, the numerical rank is often set using a threshold.
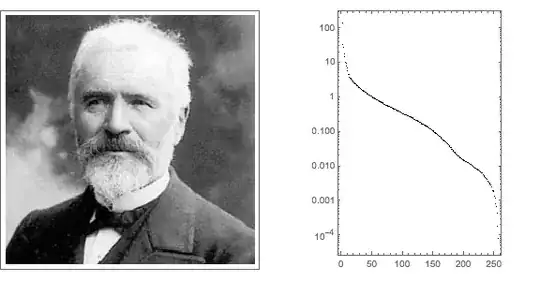
The following image of Camille Jordan is a 256 $\times$ 256 matrix of grayscale values $[0,1]$. The singular value spectrum spans seven orders of magnitude. In this example, the smallest value is much larger than machine epsilon.
However, more demanding spectra will have values near machine epsilon. The question is then whether a small number is a numeric zero or a legitimate member of the spectrum.
In practice, you might clip any singular values below, say, $10^{-11}$. In Meyer's book, p. 417, he shows how the singular values quantify how close the target matrix is to a matrix of higher rank. When the singular value is small, the target matrix is close to a matrix of higher rank.
- 10,342
-
Is the number of zero eigenvalues equal to the number of zero singular values ? – Fareed Abi Farraj Jul 15 '19 at 07:50
-
1@Fareed AF: By construction, the singular values are $>0$. The rank is the number of nonzero singular values. The issue is ticklish in computation, because zeros will manifest as small numbers, and small numbers may be uncomfortably close to machine epsilon. For a matrix $\mathbf{A}\in\mathbb{R}^{m\times n}_{\rho}$, there will $\rho$ singular values. The matrix $\mathbf{A}^{T}\mathbf{A}$ will have $n$ eigenvalues, of which $n-\rho$ are zero. – dantopa Jul 15 '19 at 20:35