2

i need you help in solving the following problem:

given the "center form" of ellipsoid:

  • A : matrix of d*d where d is the dimension
  • c : center of the ellipsoid hold in a vector

how can i compute the tilt/angle of the ellipsoid from these two inputs in Matlab?

Thanks in advance.

user3492773
  • 593

2 Answers2

1

Find the eigenvectors of $A$: they define the principal axes of the ellipsoid. From those you can compute any angles of those axes you care to.

You can find a detailed description on p.10ff of the document "Algorithms for Ellipsoids" by Stephen Pope (PDF download).

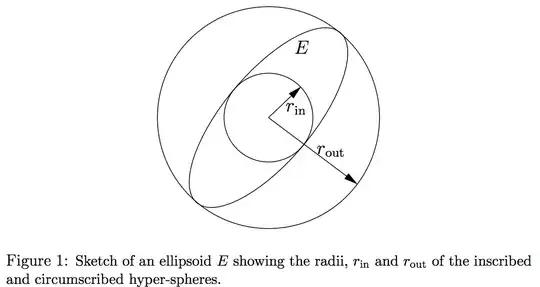
          PopeFig1
Joseph O'Rourke
  • 30,327
  • i still dont follow, i need to compute the angle of one ellipse regarding the axes, i mean i need to find the tilt of the ellipse. by the following operation i get the radiuses of the ellipse and it's orientation: [U,D,V] = svd(A); where D hold the radiuses (by inverting the values on the diagonal) and V is the orientation matrix but how can i compute the angle itself? – user3492773 Sep 07 '15 at 23:43
  • @user3492773: The eigenvectors are the ellipsoid axes. You can find the angle between two vectors---one an ellipsoid axis, another the coordinate axis of interest---via their dot product. – Joseph O'Rourke Sep 07 '15 at 23:45
  • can you give an equation please? – user3492773 Sep 07 '15 at 23:46
  • @user3492773: See "Angle between two vectors in n-space." – Joseph O'Rourke Sep 07 '15 at 23:54
  • so the angle of ellipse is equal to the sum of all angle between combination of ellipsoid axes and the coordinate system axes? – user3492773 Sep 08 '15 at 00:09
  • @user3492773: I think I cannot help more. We are talking past one another. Sorry! – Joseph O'Rourke Sep 08 '15 at 00:10
  • wait i just want to understand how can i compute the angle of the ellipse with regarding the system coordinate system. i assume e1 = [1,0] and e2 = [0,1] , and v1,v2 are ellipsoid axes. from here, how can i compute the desired angle? – user3492773 Sep 08 '15 at 00:16
1

I would like to add some more simple and practical examples to the one provided by Joseph O'Rourke.

So as explained you need 1st to find eigenvectors from A, in Matlab, there is an 'eig' command. But in order to understand what you are doing, you can find a practical example in the document by Peter O. Brown "Ellipse and Linear Algebra" starting with page 5.

In order to get eigenvector representing a semimajor axis of an ellipse, take eigenvalue with smaller absolute value. Next, you need to calculate an angle between eigenvector and (e.g.) x-axis. One of simplest explanations about how to do that could be found here or google for more pro one.

Gujche
  • 111