6

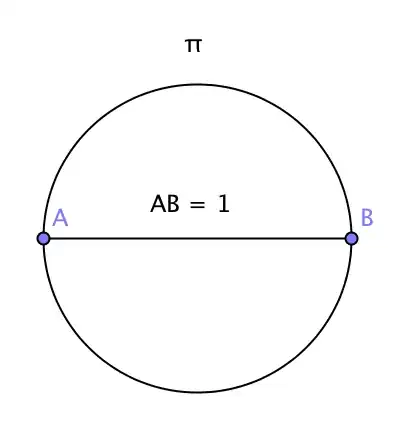
a) Let's say I have a circle with a diameter $1$. Then a perimeter is $π$ (pi) and ratio between a perimeter and a diameter is $π$.

PI

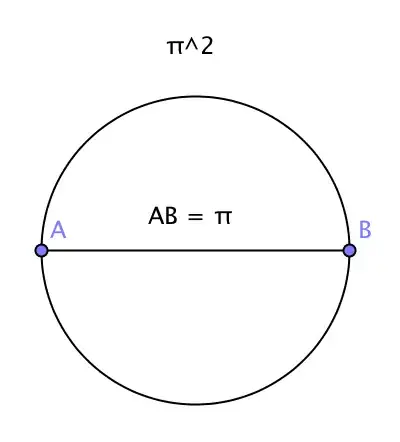
b) I want to use π as a diameter of another circle, which gives a perimeter of $π*π = π^2$ and a ratio $\frac{π^2}{π} = π$.

PI squared

My question is if there are ways to illustrate a progression from a) to b) by continuous geometrical construction. Or, how would you illustrate $π$ squared by geometry?

Added background information

I was thinking if this could be done because fractions can be presented by infinite geometric series, which is true for pi as well (Euler?):

a)

$$\pi =\sqrt{ 6\sum_{i=1}^\infty \frac{1}{i^2}}$$

b)

$$\pi^2 = 6\sum_{i=1}^\infty \frac{1}{i^2}$$

respectively to pictures above.

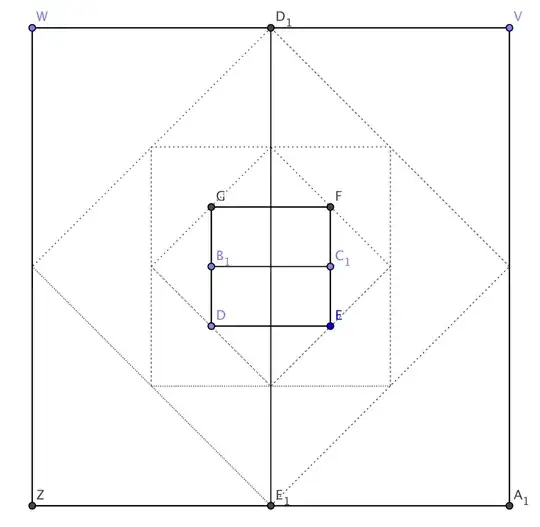
So why this geometric serial representation:

Quadrupling

where (perimeter / diagonal ratio = 4):

c) perimeter (D,E,F,G) = 4 AND diagonal (B1,C1) = 1

d) perimeter (V,W,Z,A1) = c) perimeter squared = 4^2 = 16 AND diagonal (D1,E1) = 4

is fundamentally different from a) and b) which can be expressed as geometric series?

Other background for question is my wondering what does it really mean in real world physics when you use pi squared on equations like centripetal acceleration formula:

$$\frac{T2}{R3} = \frac{4\pi^2}{GM_{central}}$$

but it is really a side matter in this case.

Update 2:

Akiva Weinberger pointed out these practical formulas for pi squared:

  • The surface area of a torus (donut shape) is $4π^2Rr=(2πr)(2πR)$
  • The volume $2π^2Rr^2=(πr^2)(2πR)$

For Euler equation I found this interesting figure, which is not exactly a progression I was asking, but a progression altogether visual and guide giving:

Quadrature

Source: http://mathart.livejournal.com/24013.html

MarkokraM
  • 671
  • 2
    What do you mean by "continuous geometrical construction"? Compass and straightedge in Euclidean geometry? It is well-known that pi and thus pi squared are transcendental numbers and are therefore not constructible by classical means. – Rory Daulton Sep 07 '15 at 12:40
  • Good point. I was thinking compass and straightedge. But neoclassical way is find as well. And answer to why pi can be shown but pi square cannot by classical means would be great. – MarkokraM Sep 07 '15 at 13:02
  • Although so obvious it is now, I didn't think this as a squaring a circle problem in first place. But it seems to be so. I will add a detail of "continuos geometrical construction" to the original post to give some background information perhaps needed for better answer position. – MarkokraM Sep 07 '15 at 15:24
  • 1
    The surface area of a torus (donut shape) is $4\pi^2Rr=(2\pi r)(2\pi R)$, where $R$ and $r$ are as in here. – Akiva Weinberger Sep 07 '15 at 18:47
  • The volume is $2\pi^2 Rr^2=(\pi r^2)(2\pi R)$. – Akiva Weinberger Sep 07 '15 at 18:52
  • As described in this answer, powers of an arc-length can be viewed as lengths of successive involutes. In particular, the involute of a half-circle has length $\pi^2/2$. – Blue Aug 07 '16 at 23:05

2 Answers2

2

Diameter and circumference increased by $\pi$ times for the second circle. Area ratio is $\pi^2.$

Pi times Circ

Narasimham
  • 40,495
1

The Euler formula you mention (b)

reminds me of Ford circles.

Ford Circles

As the radius of each circle is 1/2q² where q is the denominator of the fractions in the circles.

So, how about the sum of these radii as an image of pi²:

pi squared

Simon G
  • 65