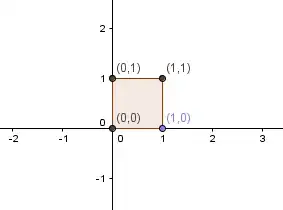4

Given the $2\times2$ matrix,

$$A=\begin{pmatrix} a & b \\ c & d \\ \end{pmatrix}$$

$\det(A)=ad-bc$

and the matrix, $$B=\begin{pmatrix} 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ \end{pmatrix}$$
which can represent a square with the vertices $(0,0),(1,0),(0,1)$ and $(1,1)$

Square with Area 1

the matrix given by multiplying them,

$$AB=\begin{pmatrix} 0 & a & b & a+b \\ 0 & c & d & c+d \\ \end{pmatrix}$$

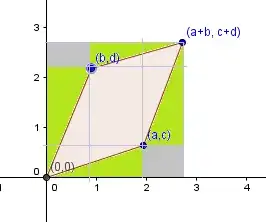
can represent a parallelogram with vertices, $(0,0),(a,c),(b,d)$ and $(a+b,c+d)$

transformed parallelogram

What I would like to do is to show that the area of this parallelogram is given by $$\det(A)=ad-bc$$.

It really boils down creating a general formula for the area of the parallelogram, and showing that it reduces to $ad-bc$.

I've started by calculating the area of the rectangle bounded by $(0,0)$ and $(a+b, c+d)$, which is $(a+b)(c+d)= ac+bc+ad+bd$.

Next, I've subtracted the areas of the figures that I've filled in with colours. Like colours don't imply like areas. Starting with the green triangle bounded by $(0,0)$ and $(a,c)$, and working counter clockwise, these are:

$ac;\; \frac{1}{2}bd;\; \frac{1}{2}ac;\; b(c+d)=bc+bd;\; \frac{1}{2}bd$

Subtracting these values from the original area:

$$ac+bc+ad+bd -\frac{3}{2}ac -2bd -2bc = ad-bc $$(minus a bunch of other stuff that shouldn't be there).

I suspect that my method is correct, but that I've either misrepresented the smaller areas or I've fumbled when sorting them out.

Can anyone please help me clean this up?

Thanks!

vonbrand
  • 27,812
MathAdam
  • 3,309

2 Answers2

1

The first $ac$ is a triangle, so it should be $ac/2$.
The two grey rectangles have area $bc$ in the bottom right and $ad$ in the top left.

Empy2
  • 50,853
  • This is such a piddly problem, the mathematical equivalent of taking apart a watch and trying to keep track of all the itty bitty screws and springs. @Michael, you are right about the first $ac$ being a triangle and the bottom right grey area being $bc$. But I believe the upper left grey area is also $bc$. I've amended my final diagram, and it works out to the desired result. I will upload it shortly. Please take a look and let me know what you think. Cheers! – MathAdam Sep 07 '15 at 04:49
  • Oops, you are right. – Empy2 Sep 07 '15 at 08:06
1

I've amended the second diagram to make it easier to sort out the tangle of areas.

parallelogram with more details

The letters in bold are mark positions along the horizontal and vertical axes. The red letters mark the lengths of the line segments.

Again, reading counter clockwise from the origin, the 6 smaller areas are:

$$\frac{1}{2}ac\;\;bc\;\;\frac{1}{2}bd\;\;\frac{1}{2}ac\;\;bc\;\;\frac{1}{2}bd$$

Subtracting these 6 areas from the larger area of $ac+bc+ad+bd$ produces the desired result of $ad-bc$.

MathAdam
  • 3,309