All lines that connect a point to a sphere directly

Question

If I have a point P anywhere in space outside of a sphere of radius R, how do I identify all the points on the surface of that sphere that can be directly connected to P, such that the line segments that connect the identified points on the sphere to P do not intersect the surface of the sphere. I am looking for the limits of this portion of the sphere surface in spherical coordinates.

Just by sketching it out, you can see that it is much less than a hemisphere because drawing a line from the edge to the point usually intersects the sphere.

In 2d, the question is: How can I tell that I can reach A from D and E, but not from C?

Answer 1

For a sphere of radius $r$ and a point at a distance $d$ from the center of the sphere you can directly "see" a spherical cap. The cap is limited by the circle that is given, where the ray from $P$ to the point on the sphere has a right angle from that point to the center of the sphere. All points with a larger angle than 90° is visible, all with smaller angle is not visible. The limit is a circle at exactle 90°. Let's derive the parameters for that spherical cap, first the radius of the limit circle $a$, and the height of the cap $h$.

Here is a sketch for the derivation:

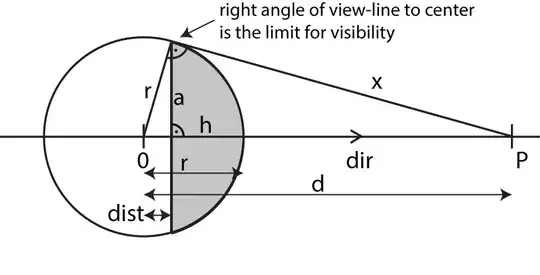
$x^2 = d^2 - r^2$

$\frac{a}{x}=\frac{r}{d}$

therefore:

$a=\frac{r}{d} \sqrt{d^2-r^2}$

From the relation

$r^2 = (r-h)^2 + a^2$

we can derive the cap height $h$ and therefore the distance from the center $r-h$:

$h = r - \sqrt{r^2 - a^2}$

$\mathit{dist} = r - h = \sqrt{r^2 - a^2}$

The direction of the center of the cap is the same as the direction from the center of the sphere to the point $P$.

The only missing point is to derive the coordinates of the circle of this cap. I assume the sphere is centered in the origin of the coordinate system. The limit circle would be given as a tilted 3D circle with the following parameters:

$dir = \frac{P}{|P|}$ (axis of 3D circle)

$center = dir * dist$

$radius = a$

You can compute the points of the circle in cartesian coordinates as described here: https://math.stackexchange.com/a/73242/264838

You can convert these points to spherical coordinates as outlined here: https://en.wikipedia.org/wiki/Spherical_coordinate_system#Cartesian_coordinates

If you only want to test a point $B$ on the sphere whether it is visible from $P$, just test for an angle >90°. You can experiment with the relationships in this Geogebra sheet: http://tube.geogebra.org/m/1564793

$\cos{\alpha} = \frac{(O - B)\cdot(P - B)}{|O - B| |P - B|}$

since $\cos{\alpha} = 0$ we just need to test

$0 > (O - B)\cdot(P - B)$

where $\cdot$ is the dot product, and $O$ is the center of the sphere, or $0$ if it is in the origin.