1

The question under debate: Is $y^4=8x^2$ a function or a relation?

We disagree. I say, it's a relation because when I substitute in points

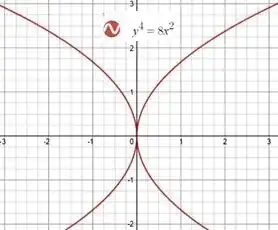enter image description here I get two outputs for most inputs, and thus it's not a function (fails the vertical line test). I also used Wolfram Alpha and Desmos to check the graph, and both of those yield vertical-line-failing horizontal parabolas... enter image description here which fail the vertical line test.

Another person says "...because the original problem did not include a root... it was an exponent - we quad-rooted the other side to solve for y only... but that wasn't the original question/problem. So the way the original problem is set up, there would be no negative answers... " which means each x has one y, it passes the vertical line test, and it’s a function.

I'll admit, I don't quite understand his reasoning, but there's a lot I don't understand, like how the square root function yields only a positive result but $x^2=9$ yields $+3$ and $-3$, so I can't argue convincingly.

Is there some way to rule either in/out? The answer given by the system indicates my answer is correct, that it's a relation and not a function, but for a host of reasons I won't describe, we don't fully trust that system.

Thank you for any light you can shed that will resolve our debate!

Robert Z
  • 145,942
sloopie72
  • 75
  • 4
    You are correct; I have no idea what your friend is attempting to say, but his conclusion is certainly wrong. – apnorton Sep 04 '15 at 18:58
  • 1
    I agree that it is a relation, and not a function, for exactly the same reasoning you say. For each $x$ there are multiple $y$'s that satisfy the equation which contradicts the definition of function which requires for each $x$ exactly one (and no more than one) $y$ satisfies the equation. – JMoravitz Sep 04 '15 at 18:59
  • 1
    As for your question, on square roots, see http://math.stackexchange.com/questions/26363/square-roots-positive-and-negative – JMoravitz Sep 04 '15 at 19:00
  • 1
    You can't determine if it is a function or relation unless you specify the domain and codomain. – Umberto P. Sep 04 '15 at 19:03
  • 1
    Why did your friend take the fourth root to solve? Equally he could have taken the negative fourth root to generate solutions. Root taking is a solution-loosing exercise; if he picks a particular branch of the locus to take solutions from, he looses the others on the lower branch. The only way to make this a function is for if you choose a value for which the upper branch equals the lower branch, that is if $x=0$. This is the only valid domain. – nathan.j.mcdougall Sep 04 '15 at 19:08

2 Answers2

5

You are definitely correct. You can regard the equation $y^4 = 8x^2$ as the relation $$xRy \iff y^4 = 8x^2,$$ and $R$ is a function of $x$ if and only if, for each $x$, there is at most one $y$ such that $xRy$. But that is clearly false in this case. For example, let $x=2$; then $y^4 = 32$ so that $y = \pm\sqrt[4]{32} = \pm 2\sqrt[4]{2}$ (as well as some complex values). Thus this relation does not define a function of $x$.

rogerl
  • 22,399
3

$y^4=8x^2$ is an equation, not a function. Moreover, this equation does not implicitely define $y$ as a function of $x$ due to the fact that more $y$'s correspond to one $x$. Also, $x$ is not a function of $y$.

On the other hand, you can consider a function $f(x,y)=y^4-8x^2$ of two variables and the domain of satisfiability of your equation equals the zero set of $f$. That is, your equation can be reformulated to $f(x,y)=0$ where $f$ is a function.

Peter Franek
  • 11,522