When $\theta$ is very small why $\sin \theta$ is similar to $\theta$ and $\cos\theta$ similar to $1$? Is it related to limits or we can prove it simply by using diagrams?
-
maybe you would like to prove $\lim_{x\to0}(\sin x - x) =0$ :-) – Math-fun Aug 26 '15 at 06:19
-
3@Math-fun How would that help? One might also prove $\lim_{x\to 0}(\sin x - x^2) = 0$ alas that does not imply $\sin x \approx x^2$,,,, – CiaPan Aug 26 '15 at 06:56
-
3@CiaPan ups you are right, thanks! one could look at the ratio $\frac{\sin x}{x}$ then turn to http://math.stackexchange.com/questions/75130/how-to-prove-that-lim-limits-x-to0-frac-sin-xx-1 – Math-fun Aug 26 '15 at 07:05
-
Yes, you can visualize it using a diagram. I have uploaded a diagram and explanation. However, this can't be called a 'proof', because a proof needs to be rigorous. – voyager Aug 26 '15 at 07:25
-
@CiaPan: Yes it does. – Aug 26 '15 at 12:55
4 Answers
Using the Taylor series expansion, we can express $\sin x$ and $\cos x$ as
$$\displaystyle\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \dots$$
$$\displaystyle\cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \dots$$
Note that when $x \ll 1$, then $x^2 \ll x$ and $x^3 \ll x^2$ and so on. Any higher powers of $x$ will be very small. Then the above functions can be approximated by their first terms.
$$\displaystyle\sin(x) \approx x $$
$$\displaystyle\cos(x) \approx 1 $$
- 10,441
On the unit circle, $\theta$ is the length of the arc (as well as the angle extended by that arc). (Thus, perimeter of the unit circle is $2\pi$). Whereas, $\cos\theta$ is the length of the $X$ intercept, and $\sin\theta$ is the length of the $Y$ intercept.
Look at the following diagram:
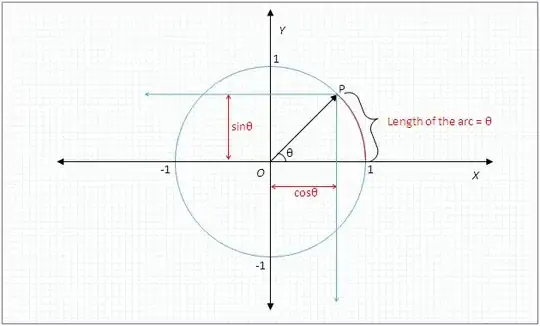
You can now easily visualize that when Point P approaches closer to $(1,0)$, then $\theta \rightarrow \ 0$. At this time, the arc in question will become almost a vertical line, and the $Y$ intercept of the arc is almost the same length as the arc.
Hence as $\theta \rightarrow \ 0$ then $\sin\theta \rightarrow \theta$
And, at that time, the length of the $X$ intercept will get closer and closer to $1$.
Hence as $\theta \rightarrow \ 0$ then $\cos\theta \rightarrow 1$
Also, from this figure, you can easily visualize that when Point P approaches $(0,1)$, the $Y$ intercept will approach $1$ and the $X$ intercept will have same length as the length of the remaining part of the arc (from point P to point $(0,1)$) which is $(\frac{\pi}{2} - \theta)$. (Remember that total length of the arc from $(1,0)$ to $(0,1)$ is $\frac{\pi}{2}$).
Thus, we have:
$\theta \rightarrow \frac{\pi}{2}$ then $\sin\theta \rightarrow 1$, and
$\theta \rightarrow \frac{\pi}{2}$ then $\cos\theta \rightarrow (\frac{\pi}{2}-\theta)$
-
-
2I am not considering the length of the arc to be $\theta$, actually it is a fact. The length of the arc of the unit circle IS taken as the angle extended by that arc, this is called Radian angle. Please refer to this: https://en.wikipedia.org/wiki/Radian. Thus, $90\textdegree$=$\frac{\pi}{2}$, and $180\degree$=$\pi$, and $270\degree$=$\frac{3\pi}{2}$, and $360\degree$=$2\pi$, and so on... – voyager Aug 26 '15 at 07:33
-
-
Yes, dear friend! A unit circle is a circle of radius 1, that's why we call it Unit Circle. That's why it intersects $X$ axis at $(1,0)$, and $(-1,0)$, and it intersects $Y$ axis at $(0,1)$, and $(0,-1)$. – voyager Aug 26 '15 at 07:41
-
-
1@voyager Apparently there is no \degree or \textdegree command in the TeX implementation on MSE. You migh use superscript circle instead — 2^\circ renders as $2^\circ$ – CiaPan Aug 26 '15 at 08:03
-
@CiaPan,, yes I was searching on various websites and trying to get the desired output. But after I experimented with a few suggestions, time ran out and my comment was blocked for further editing... You know StackExchange allows editing a comment within 5 minutes only. – voyager Aug 26 '15 at 08:41
-
@voyager When in doubt, I usually experiment with a draft answer, which has an instant preview and no time limit, and cut-and-paste to a comment space when done. :) EOT? – CiaPan Aug 27 '15 at 08:16
-
@CiaPan, thanks a lot for this helpful tip. I am a new user, and getting my head around... EOT! :-) – voyager Aug 27 '15 at 10:18
If you use circular function approach to define $\cos \theta$ then for very small but positive $\theta$, we have $\cos \theta = x$ where $x$ is the $x$ coordinate of the point on the unit circle which lies on the terminal side of the angle $\theta$. From the unit circle, you can see that as $\theta$ gets smaller and smaller, $x$ gets bigger and bigger and tends toward the point $(1,0)$ on the $x$ axis. This works like a proof of your claim.
- 77,651
See Wikipedia Small-angle approximation — Geometric:
in a right triangle the side opposite to the small angle is almost same length as the corresponding circular arc, which in turn is equal to the angle (see the definition of radian), hence sine approximately equal the angle. At the same time the long leg is almost equal to hypotenuse, making the cosine approximately equal $1$.
- 13,049