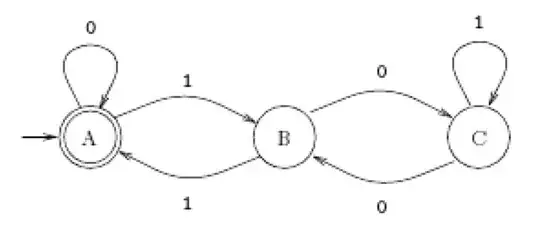
Here is another, more pedantic, approach:
Let the number $n = \sum_{k=0}^{p-1} d_k 2^k$. Define $r_k =2^k \bmod 3$, and notice that $r_k=2$ when $k$ is odd, and $r_k = 1$ when $k$ is even. Thus $n \bmod 3 = \sum_{k=0}^{p-1} d_k r_k \bmod 3$.This is the key to creating a state diagram, with the binary digits $d_0,...,d_{p-1}$ as inputs.
To compute the sum, one needs to track the existing sum (modulo 3, of course) and whether the index is odd or even (to know the value of $r_k$). So the state space is $\{0,1,2\} \times \{odd,even\}$. It is straightforward to create the state diagram with accepting states $(0,odd)$ and $(0,even)$.
$$\begin{array}{ccc}
\mathbb{state} & \mathbb{next \; state}, d_k=0 &\mathbb{next \; state}, d_k=1 \\
\hline \\
(0, odd) & (0, even) & (1, even) \\
(0, even) & (0, odd) & (2, odd) \\
(1, odd) & (1, even) & (2, even) \\
(1, even) & (1, odd) & (0, odd) \\
(2, odd) & (2, even) & (0, even) \\
(2, even) & (2, odd) & (1, odd) \\
\end{array}$$
The catch is that there are 6 states, not 3 as in the diagram above. However, if we apply the FSM Table Filling Algorithm (eg, see Hopcroft, Motwani, Ullman, "Introduction to Automata Theory, Languages and Computation") to find indistinguishable states, we find the following pairs to be indistinguishable: $\{(0,odd), (0,even)\}$, $\{(1,odd), (2, even)\}$, $\{(1,even), (2, odd)\}$. The resulting FSM is identical to the FSM above, with the state identification $A \sim \{(0,odd), (0,even)\}$, $B \sim \{(1,odd), (2, even)\}$, and $C \sim \{(1,even), (2, odd)\}$.