2

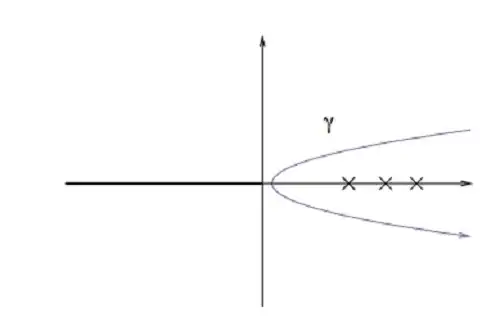
I need to perform the following integration:

$I(s) = \int_{\gamma}\text{d}z\ z^{-s} \frac{\text{d}\ln\mathcal{F(z)}}{\text{d}z}$,

where $\mathcal{F(z)}$ is analytic everywhere on the complex plane.

For the purpose of integration, the branch cut which is implied by $z^{-s}$ is chosen to be on the negative real $z-$axis, as follows.

two muppets

I understand that the function $z^{-s}$ is multivalued, but that function has $s$ complex roots over the complex plane, so should we not choose a branch that corresponds to an angle of $\frac{2\pi}{s}$ of the complex plane?

Glorfindel
  • 3,955
nightmarish
  • 617
  • "Branch corresponds to an angle" sounds meaningless to me. The question you should think about is: how can the function $z^{-s}$ be defined? The $\frac{2\pi}{s}$-sectors have to do with injectivity, not with multivaluedness (take for instance $s=2$). – Start wearing purple Aug 18 '15 at 15:51
  • Well, I understand your comment. So, carrying forward from your suggestion, I need to show that $z^{-s}$ is multivalued with $0 \leq \theta < 2 \pi$ defining a unique range. So, $z^{-s} = r^{-s}e^{-is(\theta + 2n \pi)}$. How does the power on the exponential prove the mulit-valued nature of $z^{-s}$? – nightmarish Aug 18 '15 at 16:04
  • If the function were single-valued, then its values for $\theta$ and $\theta+2\pi$ should be equal. This is not the case, that is why instead of $\theta\in \mathbb{R}$ we have to specify a domain for values of $\theta$. It is this choice of the domain which, essentially, introduces the branch cut. By the way the branch cut on the negative real axis means that the domain is chosen as $(-\pi,\pi)$. – Start wearing purple Aug 18 '15 at 16:11

0 Answers0