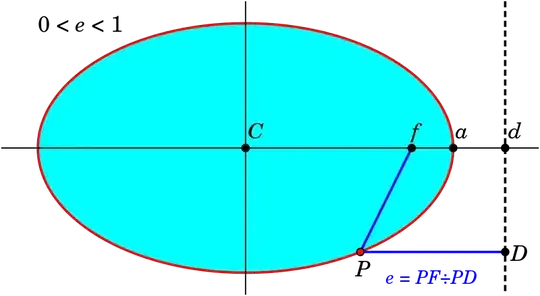
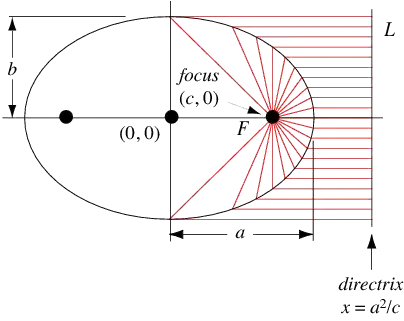
If I understood your question correctly, you're essentially asking how one can find the equation for the directrix if one only has the equation for an ellipse with a given eccentricity.
You start with the equation below
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
\qquad(1)
$$
where $a$ and $b$ are positive real-valued constants.
If you then define two points on the $x$ axis, $F$ and $F'$, by their coordinates,
$$
F \equiv (\epsilon a, 0)
\qquad(2)
$$
$$
F' \equiv (-\epsilon a, 0)
\qquad(3)
$$
for some as-yet undetermined real value $\epsilon \ge 0$, and then require that the sum of the distances from $F$ to $P$ and from $P$ to $F'$ be equal to $2a$ - for any arbitrary point $P$ on the ellipse - you'll find out that that is only possible if you choose $\epsilon$ to satisfy
$$
\epsilon = \sqrt{1 - \frac{b^2}{a^2}}
\qquad(4)
$$
So far, the above has nothing to do with the directrix. It's just a way to construct the foci and find the eccentricity, starting from some equation and then requiring that the curve described by that equation must have the fundamental property of an ellipse (namely, that the sum of the distances from any point on the ellipse to the two foci is a constant).
Now, let's see how we can prove the directrix property. Imagine that there is a vertical line at $x=d$ for some as-yet-undetermined real value $d \ge 0$ and let's see if we can find a value of $d$ such that the directrix property is satisfied. The focus for positive $x$ is $F$ (see its coordinates above), and an arbitrary point $D$ in the would-be directrix has coordinates $D = (d, y)$. The directrix property mandates that
$$
\epsilon = \frac{\overline{PF}}{\overline{PD}}
\qquad(5)
$$
Now, let's look at the square of the distances involved, since that gets rid of the square roots:
$$
\overline{PF}^{\,2} = (x - \epsilon a)^2 + (y - 0)^2 = (x - \epsilon a)^2 + y^2
$$
But $P$ lies on the ellipse so $(x,y)$ satisfies $(1)$. Therefore, eliminating $x^2$ in favour of $y^2$, but leaving the $x$ term alone, we have
$$
\overline{PF}^{\,2} =
a^2\,(1 + \epsilon^2) + y^2\,(1 - \frac{a^2}{b^2}) - 2\epsilon ax
$$
How about $\overline{PD}^{\,2}$? Note that $D$ and $P$ have the same $y$ coordinate so
$$
\overline{PD}^{\,2} = (x - d)^2 + (0)^2 = (x - d\,)^2
$$
Here's the crux now. Can we find a value of $d$ such that $(5)$ is true?
Imposing
$$
\frac{\overline{PF}^{\,2}}{\overline{PD}^{\,2}} =
\frac{a^2\,(1 + \epsilon^2) + y^2\,(1 - \frac{a^2}{b^2}) - 2\epsilon ax}{(x - d\,)^2} = \epsilon^2
$$
we get
$$
a^2\,(1 + \epsilon^2) + y^2\,(1 - \frac{a^2}{b^2}) - 2\epsilon ax = \epsilon^2\,(x - d\,)^2
$$
Note that the complicated expression above is something like this:
$$
(\mbox{terms independent of $x$ and $y$}) + (\mbox{terms involving $y^2$}) - 2\epsilon ax + 2\epsilon^2 xd = 0
$$
because the $x^2$ terms can be removed using $(1)$. Since the above has to be true for all $x$, the only hope for $(5)$ to be possible is if we choose $d$ such that
$$
2\epsilon ax - 2\epsilon^2 xd = 0
\qquad\Rightarrow\qquad
d = \frac{a}{\epsilon}
$$
With this choice, it's then not hard to show that the terms not written above also vanish so, indeed,
$$
\epsilon = \frac{\overline{PF}}{\overline{PD}}
$$
is true, provided we make that choice for $d$.
So, what's the conclusion? The conclusion is that an ellipse has two equivalent properties, namely, (A) the sum of the distances from the foci to any arbitrary point on the ellipse is a constant, and (B) the ratio of (the distance from an arbitrary point on the ellipse to one of the foci) to (the distance from that point to a fixed vertical line parallel to the semi-minor axis) is equal to the eccentricity of the ellipse.
And we also proved that $\epsilon = a/d$.
(Technically, I only proved that (A) above implies (B). We'd also have to prove that (B) implies (A) for the equivalence I referred to be proven. That's an exercise I leave for the reader...)