10

I'm sure a lot of you are acquainted with Alhazen's Billiard problem, which involves finding the point on the edge of a circular billiard table at which a cue ball at a given point must be aimed in order to canon off the edge of the table and hit another ball at a second given point.

While reading on this math problem, I thought of my favorite Marvel superhero, Captain America (Cap'). You may also know that Cap' has a special ability in which he is able to throw his shield in way so that it will ricochet off certain objects and return to him. Let's examine a scenario that places him in the context of the Billiard problem:

Cap' is standing at point C in an empty circular room. (Point C is not at the centre of the room, because if so he'd be able to throw the shield in any direction and have it bounce off the wall and return to him, since any trajectory would be the normal to the tangent at the point where the shield hits the wall. C is also not on the edge of the circle because that would lead to a trajectory based on inscribed polygons.)

At point C, to have the shield return to him with 1 richochet, all Cap' needs to do is similarly throw the shield along the line of symmetry of the room that passes through C, so we'll constrain his aim to a point not on that line of symmetry, which means we'll be looking for 2 ricochets or more.

These are the scenarios I'd like you all to consider:

Where should Cap' aim to have the shield return to him in:

  • 2 ricochets
  • 3 ricochets
  • 4 ricochets
  • n ricochets?

Edit: From the answers I've read and my own working, I believe there is a pattern for trajectories with either odd or even bounces. It would be nice if someone could algebraically find a generalized way to compute the coordinate of the ricochet point given the number of times we want the shield to bounce off the wall before returning.

Note: For sake of mathematical analysis, let's assume the shield (a point mass) always moves in a straight line, does not lose kinetic energy and obeys the Law of reflection (angle of incidence = angle of reflection.)

Razorlance
  • 275
  • 3
    For $2$ ricochets, consider the following: Take the room to be the unit circle, and note that we can always spin the room so that Cap stands on the $x$-axis; say, at point $C(c,0)$. "All you need to do" is find a point $T$ (say, above the $x$-axis) on the circle such that the the ricochet from $C$ at $T$ goes straight down (that is, perpendicular to the $x$-axis). By symmetry, the shield will ricochet at $T^\prime$ (the reflection of $T$ in the $x$-axis) and head directly for $C$. Finding $\angle COT$ in terms of $c$ is relatively straightforward. – Blue Aug 17 '15 at 08:53
  • For a circular room, think about your regular polygons and polygrams. – Neil W Aug 17 '15 at 09:14
  • @Blue yes, for 2 ricochets the obvious is to somehow create an isosceles triangle with $C$ at one vertex and 2 other vertices at the edge of the circle. But how would one go about finding $T$? – Razorlance Aug 17 '15 at 10:11
  • It might also not be necessary to rotate the room. Rather, the line of symmetry could be expressed as a parametric equation, and that would make it very easy to find $T'$. – Razorlance Aug 17 '15 at 11:08
  • 1
    Also for fun, consider that he may throw his shield with a back-handed throw, trace a regular star polygonal pattern (see https://en.wikipedia.org/wiki/Star_polygon), and catch it on the forehand side. For example, it may trace the path a 5-pointed star (Schläfli symbol {5,2}), but that has a fairly large center compared to ricochet points. A {7,3} star has a tighter center. – Michael Tiemann Aug 17 '15 at 11:15
  • 1
    @Razorlance: It's not necessary to rotate the room. Nor is it necessary to assign the room a unit radius, or center it at the origin, or even draw it in the $xy$-plane. But doing so helps, by reducing the problem to its essence; in this case, it spotlights that the only relevant parameter (other than $n$) is Cap's distance from the room's center, relative to the room's radius ... the value I call $c$. It may be "very easy" to work with a parameterized line of symmetry, but it's very very very easy to work with one that aligns with the $x$-axis. I'll take any advantage I can get. :) – Blue Aug 17 '15 at 11:46
  • @Blue, using your method I've found a formula for $∠OCT$ that depends on the the distance of $C$ from the origin of the unit circle along the x-axis. It looks like a mess though, and assumes that $C$ must be on the positive side of the x-axis. I'm not quite sure how to do the rotation transformation.

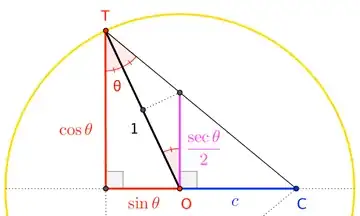
    Here's the equation: http://www.wolframalpha.com/input/?i=y+%3D+pi%2F2+-+2%282atan%28sqrt%288x%C2%B2+%2B+1%29+%2F+%282x%29+-+sqrt%281+%2F+x%C2%B2+%2B+1+%2F+%28x%C2%B2+sqrt%288x%C2%B2+%2B+1%29%29+%2B+8+%2F+sqrt%288x%C2%B2+%2B+1%29+%2B+2%29+%2F+sqrt%282%29+%2B+1+%2F+%282x%29%29%29+from+0+to+1

     – Razorlance Aug 20 '15 at 10:45
  • $y$ is $<OCT$ while $x$ the distance from the origin. – Razorlance Aug 20 '15 at 10:48
  • As we've seen now the case of two bounces is pretty straightforward. The case of three bounces is also pretty straightforward, and also has a solution of the form $\text{quadratic in}~\sin\theta = c$. In general for an even number of bounces you want the particle to be moving vertically after half the bounces, and for an odd number of bounces you want the middle bounce to be at one of the two points on the $x$-axis (if $C$ is on the $x$-axis), and this plus some geometry will give you an algebraic relationship between $c$ and $\sin\theta$. – Sean Eberhard Aug 22 '15 at 09:04
  • (continued) Are you just interested in seeing this algebraic mess in all its glory, or do you want an algorithm to numerically compute $\theta$ in terms of $c$? Maybe it's more interesting to ask a related qualitative question like this one: How many different directions can Cap shoot in such a way that the shield returns to him after exactly $n$ bounces? Ignoring the two points on the $x$-axis (which always work), and working only up to reflection in the $x$-axis, the answer is $1$ for $n=2$, $1$ for $n=3$, but I think $3$ for $n=4$. This question is much more likely to gain traction here. – Sean Eberhard Aug 22 '15 at 09:04
  • (continued) Another question: Does the answer depend on $c$? It's not obvious to me that there aren't some critical points $c$ at which the answer changes. – Sean Eberhard Aug 22 '15 at 09:05
  • I've spun this question off here: http://math.stackexchange.com/questions/1405746/trajectories-on-a-circular-billiards-table – Sean Eberhard Aug 22 '15 at 09:46

1 Answers1

6

This is basically a long comment about OP's linked solution to the $2$-ricochet case: You're right, it's a "mess". :)

Don't feel too bad, however. It took me a couple of tries to find a clean approach. A first attempt involved an irreducible cubic; the second, a cubic with an extraneous linear factor. However, a little perseverance and geometric insight finally got me to just the core quadratic relation.

Below is an illustration of (half of) the $2$-ricochet case, where Captain America stands at point $C$, distance $c$ (with $0 < c \leq 1$) from the center $O$ of a unit-radius room:

enter image description here

Here, $T$ is the first ricochet point (the second being the reflection of $T$ in $\overleftrightarrow{OC}$), and necessarily-acute $\theta$ is both the angle of incidence and reflection of the shield bouncing off of the wall at $T$. Similar right triangles in the figure give us this relation:

$$\frac{\cos\theta}{c+\sin\theta} = \frac{\sec\theta}{2c} \quad\to\quad 2 c \cos^2\theta = c + \sin\theta \quad\to\quad 2 c \sin^2\theta+\sin\theta- c = 0$$ Solving for $\sin\theta$ gives $$\sin\theta = \frac{1}{4c}\left( -1 \pm \sqrt{ 1 + 8 c^2 }\right) \qquad\to\qquad \sin\theta = \frac{1}{4c}\left( -1 + \sqrt{ 1 + 8 c^2 }\right)$$ Where the acuteness of $\theta$ allows us to replace "$\pm$" with "$+$". $\square$

(Sanity check: When Cap stands at the wall, so that $c=1$, the formula gives $\sin\theta = 1/2$. That is, $\theta = 30^\circ$, just as one would expect when $C$ and $T$ are vertices of an inscribed equilateral triangle.)

Blue
  • 75,673
  • Very elegant solution. +1 – wltrup Aug 21 '15 at 12:31
  • 1
    Very nice. Out of curiosity, what application did you use to draw the diagram? – Razorlance Aug 22 '15 at 10:26
  • 1
    This is not the only solution for $2$ bounces, at least if $c$ is sufficiently large. Here is another one: If $c>1/2$ then rotate an inscribed equilateral triangle until it passes through $C$. Now fire along the triangle. This gives two further solutions which are not symmetric in the $x$-axis. – Sean Eberhard Aug 22 '15 at 23:10
  • Sorry, of course that's 3 bounces. – Sean Eberhard Aug 22 '15 at 23:11
  • @Razorlance: Thanks! BTW, I use GeoGebra. – Blue Aug 23 '15 at 04:36
  • @SeanEberhard Given that a circle has rotational symmetry I think whether the solution is symmetrical to the x-axis or not is arbitrary since we can always rotate the room so that it is. – Razorlance Aug 23 '15 at 09:05
  • 1
    @Razorlance: When Sean describes symmetry with respect to "the $x$-axis", he means symmetry with respect to "the line joining $C$ to the origin" (which only happens to align with the $x$-axis in the convenient model). So, an asymmetric shield path in this sense would remain asymmetric upon rotating the room, the path, and the Cap'n. The point here is that shield path is a chain of chords, and it need not be the case (for $n>2$) that this Cap-line meets any of those chords at their midpoints or endpoints the way it does for $n=2$. – Blue Aug 23 '15 at 09:19
  • Hi @Blue, I've been trying to apply your method to the case of 4 bounces, but I'm totally stuck. Do you think you could you guide me through the solution for this specific case? – Razorlance Nov 01 '15 at 12:51
  • @Razorlance: I'm afraid I don't have a lot of time for this these days. I'll have to come back to it. – Blue Nov 04 '15 at 17:48