I trying to understand the proof of Proposition 2.10.5 from the book: TENSOR CATEGORIES, by P. Etingof, S. Gelaki, D. Nikshych, and V. Ostrik, See http://www-math.mit.edu/~etingof/egnobookfinal.pdf.
Proposition 2.10.5. If $X\in \mathcal{C}$ has a left (respectively, right) dual object, then it is unique up to a unique isomorphism.
Something I did not understand is why the three small squares of the following diagram commute?
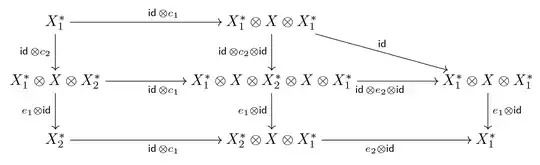
where $e_1, c_1, e_2, c_2$ the corresponding evaluation and coevaluation morphisms