5

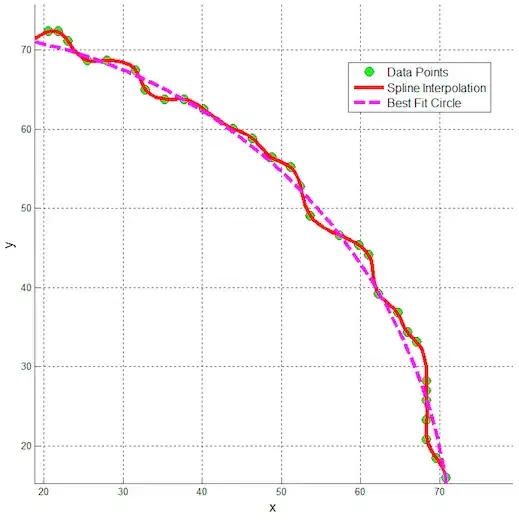
I am looking to quantify the (for a lack of a better term) "wigglyness" of a parametric curve. The particular set of curves that I am looking at come from cubic-spline interpolation on a set of points that lie, more or less, on a section of a circle (see image at the bottom).

After interpolation, I have the parameterized coordinates $x(t)$ and $y(t)$, functions of arclength, and can also easily take their 1st and 2nd derivatives. The quantity I am looking to define, then, is the amount that the curve oscillates back and forth.

I have considered simply computing the best-fit circle and letting my quantity be the mean squared error, but the problem is that although the curve certainly looks circular, I would prefer to avoid using the assumption.

My current approach is to calculate the root mean square curvature over a large number of points on the curve, using the formula for the curvature of a parametric curve $$\kappa=\frac{x'y''-y'x''}{(x'^2+y'^2)^{3/2}}$$

This approach seems to work fairly well, but it does have the problem that it seems to be influenced a fair bit by the global shape of the curve rather than the smaller local perturbations; the mean value tends to be around $\frac{1}{r}$, where r is the radius of the best fit circle.

So finally, my question is: is there a quantity that better describes the local "wigglyness" of this type of curve, rather than the global shape?

enter image description here

EDIT:

While the link provided in the comments does look like a great technique (in particular, it appears to be better than my current method), it still does not get rid of the issue of the influence of the global geometry. That is to say, there will be some default 'energy' contributed due to the general shape of the arc, whereas I am only interested in the 'energy' due to the wiggles. Perhaps, sticking with the energy analogy, I can simply subtract off this default energy to obtain the quantity of interest?

Jonathan Doucette
  • 53
  • Related, maybe regardable as duplicate. Although the answer there might even better fit here. – ccorn Aug 12 '15 at 22:23
  • 1
    Actually, the root-mean-square curvature is $\sqrt{2W}$, if the mean is calculated as an integral (which can be simplified to something close to a point sum as shown there). So those two approaches are essentially the same. (Update: Not exactly, yours is the more general nonlinear parameterized version.) Regarding the contribution of the general shape, you can estimate its influence. You know that longer-wavelength wiggles drop in amplitude inversely squared when you take the second derivative, so there is a low-pass filter effect associated with the method. – ccorn Aug 12 '15 at 23:14
  • I have retracted my duplicate flag, as this is a 2D parametric problem and tries to deal with nonlinearized curvature. An appropriate solution may be analogous, but not identical, and probably more general. – ccorn Aug 12 '15 at 23:21
  • This might also interest you. Would need adaptation to your problem, but it has an idea of what unnecessary wiggles are: Those whose turns are essentially undone by other wiggles. To filter them out, penalize the total variation. Caution: Nonlinear equations, implementation needs to be iterative and needs detail considerations, but is quite successful in the "noise removal" business. Has been adapted to clean up 2D satellite imagery. – ccorn Aug 12 '15 at 23:44
  • However, the total variation penalization favors results with piecewise straight line segments, so derivatives have singularities at the joints. If you need derivatives, better stay with a properly adapted elastic spline analogy, I'd say. – ccorn Aug 12 '15 at 23:57
  • Thanks for all of your comments! They have been very helpful. And yes, I agree; TV penalization seems very interesting but I do need derivatives, so I will see how I can adapt the elastic spline technique – Jonathan Doucette Aug 13 '15 at 00:47

2 Answers2

3

I think the right approach is to look at variation of curvature. For a circle, this variation will be zero, and for "wiggly" curves, it will be large. Constructing a spline curve that minimizes this variation is a fairly nasty non-linear problem, but just measuring the variation for a given curve is not too hard.

Carlo Sequin's group have done quite a bit of work on various measures of "energy" or smoothness in curves. Here is one reference that specifically talks about minimization of curvature variation. The abstract says:

Where traditional fairness measures are based on strain energy, we have developed a better measure of fairness; the variation of curvature. In addition to producing objects of clearly superior quality, minimizing the variation of curvature makes it trivial to model regular shapes such as, circles and cyclides.

More generally, folks in the field of CAGD (Computer-Aided Geometric Design) are always making up new/different measures of smoothness, in an attempt to quantify the aesthetic "fairness" or beauty of curves and surfaces.

bubba
  • 43,483
  • 3
  • 61
  • 122
0

Try finding the area between the interpolation and the best fit circle line in this way: sum up the area between the two lines until you get 0 and then you could use that length from the lower boundary of the integral to the upper boundary as a "wavelength" and then you can calculate the frequency at which it oscillates.

I don't know if this it the correct way of doing such things, just a wild guess.

Darawan
  • 5