Let $X$ be a complete metric space and $f:X \to X$ be bijective and a connected preserving map i.e. $f$ carries every connected set of $X$ to a connected set of $X$ ; then is it necessarily true that $f^{-1}$ also carries connected sets to connected sets ?
Asked
Active
Viewed 168 times
4
-
So are you supposing that $f$ is bijective? – Crostul Aug 12 '15 at 16:32
-
Related: http://math.stackexchange.com/questions/952466/does-there-exist-a-bijection-of-mathbbrn-with-itself-such-that-the-forward – Mizar Oct 28 '15 at 13:52
1 Answers
9
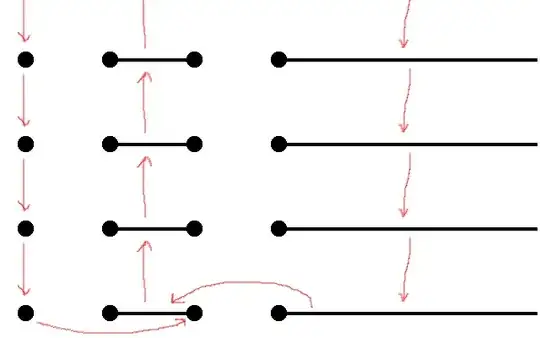
Let $$X=\bigl(\{-2\}\cup [-1,0]\cup [1,\infty)\bigr)\times \Bbb N_0$$ with the induced metric as a subspace of $\Bbb R^2$. This space is complete. The connected subspaces are precisely those of the form $I\times\{n\}$ where $n\in\Bbb N_0$ and either $I=\{-2\}$ or $I$ is an interval $\subseteq [-1,0]$ or $I$ is an interval $\subseteq [0,\infty)$.
Consider the map $f\colon X\to X$ given by $$f(x,y)=\begin{cases}(-\frac1x,y)&\text{if $x>0$ and $y=0$}\\ (0,0)&\text{if $x=-2$ and $y=0$}\\ (x,y+1)&\text{if $-1\le x\le 0$}\\ (x,y-1)&\text{otherwise.}\end{cases} $$ This is a continuous bijection and preserves connectedness. But its inverse maps the connected set $[-1,0]\times \{0\}$ to the not connected set $\bigl(\{-2\}\cup [1,\infty)\bigr)\times\{0\}$.
The thing works a bit like a zipper:
Hagen von Eitzen
- 374,180
-
If I'm not mistaken , the inverse map is $f^{-1}(z)=\sqrt z$ , which is continuous , and hence connected preserving – Aug 15 '15 at 13:44
-
-
1@SaunDev The bijectivity condition was added to the problem statement a day after my answer was posted ... – Hagen von Eitzen Oct 25 '15 at 12:54
-
-
-