The gamma distribution with parameters $\alpha$ and $\beta$ is:
$$f(x) = \frac{1}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha - 1} e^{-x/\beta}$$
When we substitute $\alpha = r/2$ and $\beta = 2$, we get the Chi-Square distribution. Why do we call $r$ the degree of freedom of $X$? Why the term "freedom"?
This is a historical name for the shape parameter of a chi-squared distribution.
Suppose we have a dataset $X_1, \dots, X_n$ from a normal distribution with unkinown mean $\mu$ and unknown variance $\sigma^2$. Then then the sample variance is defined as $S^2 = \frac{\sum_{i=1}^n (X_i - \bar X)^2}{n-1},$ where $\bar X$ is the sample mean. The sample variance is used to estimate the population variance $\sigma^2.$ In that case $Q = (n-1)S^2/\sigma^2 \sim Chisq(DF = n-1).$
Roughly, the proof begins by regarding the data as a vector in $n$-dimensional space. The sample mean represents one linear restriction on the data, leaving $n-1$ dimensions "free" to represent the variance. The term 'degrees-of-freedom' frequently stands for dimensionality.
If $\mu$ were known, then the quantity $V = \frac{\sum_{i=1}^n (X_i - \mu)^2}{n}$ might be used to estimate the population variance $\sigma ^ 2$. In this simpler case $$nV/\sigma^2 = \sum_{i=1}^n \left(\frac{X_i - \mu}{\sigma}\right)^2 = \sum_{i-1}^n Z_i^2 \sim Chisq(DF = n),$$ where the $Z_i$ are iid standard normal. (It is easy to show with generating functions that the sum of squares of $n$ independent standard normals in chi-squared.)
So one often says that we have "lost one degree of freedom" for estimating $\sigma^2$ because of the need to estimate $\mu.$
A more elementary (if less complete) explanation is that we divide by $n-1$ in the definition of $S^2$ because $\sum_{i=1}^n (X_i = \bar X) = 0.$ Hence only $n - 1$ of the deviations $(X_i - \bar X)$ from the mean are "free" to vary.
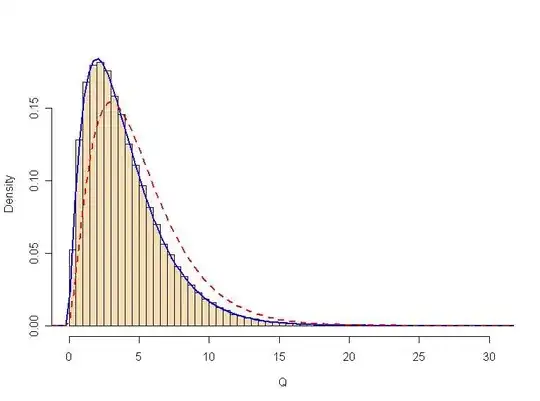
Below is a brief simulation using 100,000 samples of size $n=5$ from the distribution $Norm(\mu=100, \sigma=15).$ It shows that the simulated distribution of $Q$ is $Chisq(DF = 4)$ [blue density curve] and not $Chisq(DF = 5)$ [broken red curve].
m = 10^5; n = 5; mu = 100; sg = 15
DTA = matrix(rnorm(m*n, mu, sg),nrow=m) # each row a sample of 5
s.sq = apply(DTA, 1, var)
mean(s.sq)
## 225.123 # sim E(sample var) close to pop var 225
Q = (n-1)*s.sq/sg^2
mean(Q)
## 4.002187 # sim E(Q) close to mean of Chisq(4)
