For the case where $n = 2$: Take fixed numbers $x_0, x_1, a_0$, and $a_1$. Let's look at a few special cases.
Say we want a polynomial $Q$ such that $Q(x_0)$ is $a_0$ while $Q(x_1) = 0$.
Since $x_1$ is a root, we can say that $Q(x) = c(x-x_1)$ for some coefficient $c$. Then we have $a_0 = Q(x_0) = c(x_0-x_1)$. Solve this for $c$, and we find that
$$Q(x) = c(x-x_1) = \frac{a_0}{x_0-x_1}(x-x_1) = a_0\frac{x-x_1}{x_0-x_1}.$$
Now say we want a polynomial $R$ such that $R(x_0)$ is $0$ while $R(x_1)$ is $a_1$. Through similar reasoning, we get that
$$R(x) = a_1\frac{x-x_0}{x_1-x_0}.$$
Notice that we $Q(x) + R(x)$ satisfies the conditions that you put on your polynomial $P_1(x)$. So we finally have
$$P_1(x) = Q(x) + R(x) = a_0\frac{x-x_1}{x_0-x_1} + a_1\frac{x-x_0}{x_1-x_0}.$$
(Furthermore, it's possible to prove that there is at most one polynomial that fits the chosen points, and hence this solution is unique.)
EDIT: For anyone reading this now, the author of this question had asked for a derivation of the formula for a Lagrange interpolating polynomial given two points. Now the author has edited his question to ask for a derivation of the general formula. The derivation I gave here can easily be extended to this situation.
Say we want a polynomial $P_0$ such that $P_0(x_0) = a_0$ while $P_0(x_1), P_0(x_2), \ldots , P_0(x_n)$ are roots. Knowing all these roots, we can say that $P_0(x) = c(x-x_1)(x-x_2)\ldots(x-x_n)$. Then we have $a_0 = P_0(x_0) = c(x_0-x_1)(x_0-x_2)\ldots(x_0-x_n)$. Solve for $c$ to find that
$$P_0(x) = c(x-x_1)(x-x_2)\ldots(x-x_n) = a_0\frac{(x-x_1)(x-x_2)\ldots(x-x_n)}{(x_0-x_1)(x_0-x_2)\ldots(x_0-x_n)}.$$
Do the same for each of the other points -- that is, for each natural number $k$ where $0 \leq k \leq n$, find the equation for a polynomial $P_k$ such that $P_k(x_k) = a_k$ and all the other $x_0, x_1, \ldots, x_n$ points are roots. Then simply sum all these polynomials to get a final polynomial that hits each of the desired points.
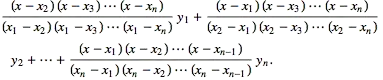 $$=> P(x) = P(x_1) \frac {x-x_0}{x_1-x_0} + P(x_0) \frac {x-x_1}{x_0-x_1}$$" />
$\tag 9$
$$=> P(x) = P(x_1) \frac {x-x_0}{x_1-x_0} + P(x_0) \frac {x-x_1}{x_0-x_1}$$" />
$\tag 9$