Best fit ellipsoid

Question

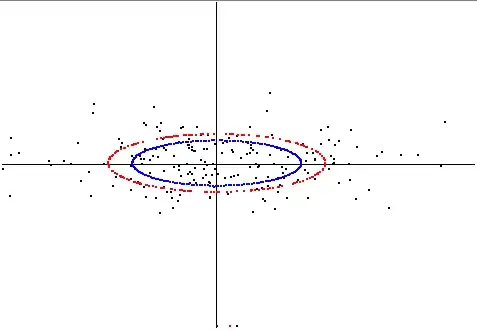
Given a collection of points $P \subset \mathbb R^3$, a crude characterization of the "shape" of $P$ is sometimes given by the principal components. We construct a covariance matrix, e.g., if $P$ is discrete, $C = \displaystyle\sum_{p\in P} (p - \mu)(p - \mu)^\intercal$, where $\mu = \displaystyle\frac1{|P|}\sum_{p\in P}\, p$ is the centre of mass. This defines an ellipsoid whose semi-axis are defined by the unit eigenvectors of $C$, scaled by the associated eigenvalues.

My question is concerned with the following statement:

The ellipsoid described by the principal components is the best fit ellipsoid for $P$.

Unfortunately, I don't know of any author or resource that I can accuse of explicitly making such a claim$^*$. Anyway, my question is:

Is there a natural geometric definition of "best fit ellipsoid" for which the above statement becomes true?

For example, some kind of least squares or other variational characterization of this same ellipsoid is what I am looking for. I would also accept an answer that convinces me that this is the wrong way to be looking at the principal components, but that will be a tough sell.

If we do a coordinate translation, so that $v_p = (p - \mu)$, and let $\hat{v}_p = \frac{v_p}{\left\|v_p\right\|}$, and look at $C$ as a linear transformation which is the sum of the rank one operators in this coordinate system, $C = \displaystyle\sum_{p \in P} \left\|v_p\right\|^2 \hat{v}_p\hat{v}_p^\intercal$, then the ellipsoid in question is the image of the unit ball. From this characterization I gain some intuition as to why this particular ellipsoid is a good one. I am looking for a better understanding, preferably from a geometric perspective.

---

* Wikipedia comes close to such a claim in the description of the moments: "The 'second moment', ... in higher dimensions measures the shape of a cloud of points as it could be fit by an ellipsoid."

---

---

Edit: Although I feel that the observation that the ellipsoid reflects the variance of the Gaussian distribution that has maximal likelihood to produce $P$ (I haven't rolled up my sleeves and checked), this is not the kind of answer I am looking for. Perhaps I should remove all tags that refer to probability or regression.

I will make the question very specific then. From stuff I've seen elsewhere on the web, I get the feeling that this ellipsoid is different from the one that minimizes the sum of squared distances to the points, but I don't know for sure.

How about this then: the radial distance from a point $p$ to the ellipsoid is the distance as measured along the line that contains $p$ and $\mu$ (the latter being the origin in our new coordinate system). So let this be my question:

Does the ellipsoid defined above minimize the sum of the squared radial distances?

Answer 1

From the principle of the "jacobi-rotation" method for obtaining the principal components it is clear, that some ellipsoid (based on the data) is defined by the following idea:

twodimensional case:

1. rotate the cloud of datapoints such that the sum-of-squared x-coordinates ("ssq(x)") is maximum

2. the sum-of-squared y-coordinates ("ssq(y)") is then minimal.

multidimensional case:

1. you do 1) with all pairs of axes x-y, x-z, x-w,... This gives a "temporary" maximum of ssq(x)

2. then you do 1) with all pairs y-z,y-w,... to obtain a "temporary" maximum of ssq(y) and so on with z-w,....

3. Then you repeat the whole process until convergence

In principle this only defines the direction of the axes of some ellipsoid. Then, for instance in the monography "Faktorenanalyse" ("factoranalysis") of K. Ueberla, the size of the ellipsoid is defined by: "length of the axes are the roots of ssq(axis)" (paraphrased) Here no direct reference is made to the property of radial deviation (when representated in terms of polar-coordinates).

In fact, the concept of minimizing the radial distances is different by a simple consideration.
If we have -for instance- only three datapoints which are nearly on one straight line, then the center of the best-fitting-circle tends to infinity and not to the mean. The same may occur with some cloud of datapoints whose overall shape is that of a small but sufficient segment of a circumference of an ellipse. Well, we may force the origin into the arithmetic center of the cloud - but this introduces a likely artificial restriction. Actually, if you search for "circular regression" you'll arrive at nonlinear, iterative methods much different of the method of principal components.

[update] Here I show the difference between the two concepts in a two-dimensional example. I generated slightly correlated random-data. Rotated to pca-position, such that the x-axis of the plot is the first princ.comp. (eigenvector) and so on.

The blue ellipse is that ellipse using the axis-lengthes of stddev of the principal components.

Then I computed another ellipse by minimizing the sum-of-squares of radial distances of datapoints to the ellipses circumference (just manual checking), this is the red ellipse. Here is the plot:

[end update]

---

One more comment for the geometric visualization (it is just for the two-dimensional case).

Consider the cloud of data as endpoints of vectors from the origin. Then the common concept of the resultant is the mean of the arithmetic/geometric sum of all vectors. This is also called "centroid" and in early times of factor-analysis, without the help of computers, it was often an accepted approximation for the "central tendency": the mean of the coordinates are the best fit in the sense of least "squares-of-distances" .

However, if some vectors have "opposing" (better word?) direction, their influence neutralizes, although they would nicely define an axis. In the old centroid-method such vectors were "inflected" (sign changed) to correct for that effect.

Another option is to double the angle of each vector - then opposing vectors overlay and strengthen each others influence instead of neutralizing. Then take the mean of the new vectors and half its angle. This is then the principal component/axis and thus represents another least-squares estimation for the fit. (The computation of the rotation-criterion agrees perfectly to the minimizing formula of the Jacobi-rotation for PCA)

Answer 2

Just fleshing out Rahul's comment: probably this choice of $\mu$ and $\Sigma$ maximizes the likelihood of the points given a multivariate Gaussian distribution $N(\mu,\Sigma)$.

Answer 3

You answered your own question: best fit by principal components is a fitting method. You simply need to trust this method and study its properties.

For example: forget about incomplete, poorly sampled data. Assume there is plenty of uniformly sampled data [whichy is true in many applications, like ellipstometry]. If that data comes from an ellipse, then its principal components are the same as those of the best fit ellipse. If the data does not come from an ellipse then questions about goodness of fit become increasingly meaningless - or application dependent.