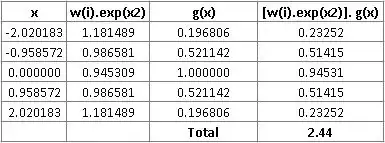
I'm trying to learn Gauss Hermite Integration and was manually try to calculate the value of integral of $\frac{1}{1+x^2}$ from $-\infty$ to $+\infty$ The exact answer is simply $\pi$ ($\approx$ 3.14). But I keep getting answers that are a bit far off even with 5 nodes. Below are my calculations, could somebody please point anything obviously wrong or may be the method is more accurate for certain kind of functions.
Edit: even with 100 nodes, I only got as close as 2.93.
I got weights from - http://www.efunda.com/math/num_integration/findgausshermite.cfm