I'm learning trigonometric substitutions and am having a bit of trouble understanding the intuition behind the conversions (why do most use secant?). If you could explain the conversions geometrically using a triangle, that would be very helpful. For example, if we have $$\int \frac{\sqrt{x^2-4}}{x}\,dx$$ I tried to construct a triangle like so:
To get $$\sin(\theta)=\frac{\sqrt{x^2-4}}{x}$$
But this is incorrect for use as a substitution. Why?
I think the way to think about trigonometric substitutions is to remember the fundamental result that
$$\sin^2a + \cos^2a = 1$$
for any angle $a$. So, in your example, you have a square-root
$$\sqrt{x^2 - 4}$$
Imagine for a moment that that 4 was a 1 and that they were reversed, like so:
$$\sqrt{1 - x^2}$$
Then the substitution $x = \sin\theta$ would result in something simple, without the square-root, namely
$$\sqrt{1 - x^2} = \sqrt{1 - \sin^2\theta} = \cos\theta$$
That's the gist behind trig substitutions.
Now, in your case in particular, things aren't so simple so let's work it out step by step. First, imagine the 4 is a 1:
$$\sqrt{x^2 - 1}$$
We can't use $x = \sin\theta$, nor $x = \cos\theta$, here because we'd get the square-root of a negative quantity. For instance, using $x = \sin\theta$,
$$\sqrt{x^2 - 1} = \sqrt{-\cos^2\theta}$$
So how can we use the fundamental relation at the top of this post to get something like $x^2 - 1$? Well, divide both sides by $\cos^2a$ and write it as follows:
$$\frac{\sin^2a}{\cos^2a} + \frac{\cos^2a}{\cos^2a} = \frac{1}{\cos^2a} \quad \rightarrow \quad \tan^2a = \frac{1}{\cos^2a} - 1 = \sec^2a - 1$$
Now it's obvious that $x = \sec\theta$ give us
$$\sqrt{x^2 - 1} = \sqrt{\sec^2\theta - 1} = \sqrt{\tan^2\theta} = \tan\theta$$
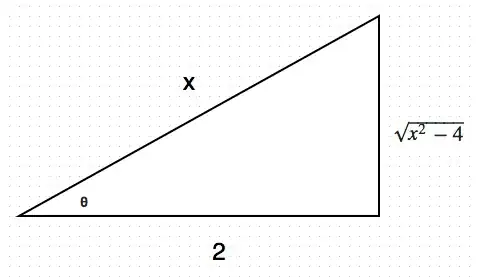
and we once again got rid of the square-root. The only thing that remains is the 4. We can deal with that by scaling. Choose $x = 2\sec\theta$, instead, so
$$\sqrt{x^2 - 4} = \sqrt{4\sec^2\theta - 4} = \sqrt{4(\sec^2\theta - 1)} = \sqrt{4\tan^2\theta} = 2\tan\theta$$
So, to summarise, all you really need to remember is the fundamental relation at the top of this post and "massage" it as necessary to get rid of any square-roots that are in your way.
The two main forms that you'll use are:
$$\sin^2a + \cos^2a = 1$$
and
$$\tan^2a + 1 = \sec^2a$$
which, as we've seen, are really one and the same.
The intuition to use trig-sub is because sometimes a problem becomes easier when you make substitutions. Mainly, grouping "nasty" looking quantities into neat little packages can save you a headache. Notice that where you placed the quantities "$2$" and "$\sqrt{x^2-4}$" in your picture were arbitrary. Try switching them and see what happens. Your answer will still be correct.
The idea is to eliminate the square root. For $\sqrt{x^2+a^2}$, the substitution $x=a\tan t$ makes the square root
$$\sqrt{a^2\tan^2t+a^2}=\sqrt{a^2\sec^2t}=\pm a\sec t$$
Similarly, $x=a\sin t$ eliminates the square root for the form $\sqrt{a^2-x^2}$. Your example is the third case, $\sqrt{x^2-a^2}$. So this time secant eliminates the radical.
$$x=2\sec t,dx=2\sec t\tan tdt$$
The integral now becomes
$$\int\frac{\sqrt{4\sec^2t-4}}{2\sec t}2\sec t\tan tdt=$$ $$\int\pm2\tan^2tdt$$
One more trig identity and the integral is easily solved. I believe the sign issue is usually ignored, though it may come into play for definite integrals based on the bounds.
It's not that it's wrong to take on the integral the way you propose -- it's just not awfully convenient. If we implicitly differentiate your substitution equation, we obtain
$$ \cos \theta \ d\theta \ = \ \frac{x \ \cdot \frac{1}{2} \ (x^2 - 4)^{-1/2} \ \cdot 2x \ - \ (x^2 - 4)^{1/2} \ \cdot \ 1}{x^2} \ dx $$ $$ = \ \frac{4}{x^2 \ (x^2 - 4)^{1/2}} \ dx \ = \ \left(\frac{2}{x} \right)^2 \cdot \ \frac{2}{ \ (x^2 - 4)^{1/2}} \ \cdot \ \frac{1}{2} \ \ dx $$ $$ = \frac{1}{2} \ \cdot \ \cos^2 \theta \ \cdot \ \frac{1}{\tan \theta} \ \ dx $$
[using your right triangle]
$$ \Rightarrow \ \ dx \ = \ 2 \ \tan \theta \ \cdot \ \frac{\cos \theta}{\cos^2 \theta} \ \ d\theta \ = \ 2 \ \tan \theta \ \sec \theta \ \ d\theta \ \ , $$
which is just the result Mike shows. Following your lead, the integral becomes
$$ \int \ \sin \theta \ ( \ 2 \ \tan \theta \ \sec \theta \ \ d\theta \ ) \ = \ 2 \int \ \sin \theta \ \tan \theta \ \frac{1}{\cos \theta} \ \ d\theta \ = \ 2 \int \ \tan^2 \theta \ \ d\theta \ \ . $$
There are easier ways to get there, though.
