When $X,Y$ are iid random variables, uniformly distributed on $[0,1]$, then $Z=X*Y$ has the density $-\log(z)$, as it is shown here:
product distribution of two uniform distribution, what about 3 or more
The question is: For which density of $X,Y$ is the product $Z$ uniformly distributed on $[0,1]$?
Let $W_1,W_2$ be independent Gamma random variables with $\alpha=1/2$ and $\beta=1$. Then $e^{-W_1}\,e^{-W_2}=e^{-(W_1+W_2)}$ where $W_1+W_2$ is exponential with mean 1. An easy transformation argument shows that $e^{-(W_1+W_2)}$ has a uniform(0,1) distribution.
$e^{-W_1}$ and $e^{-W_2}$ are i.i.d. random variables whose product is uniform(0,1).
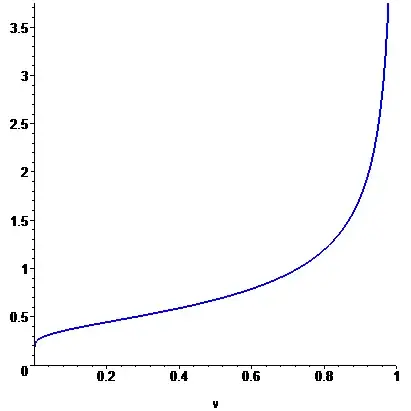
What kind of density does $e^{-W}$ have? The density of $W$ is $f(w)={1\over\sqrt{\pi w}}\, e^{-w}\, {\bf 1}_{(0,\infty)}(w).$ Setting $X=e^{-W}$, we have $|dw/dx|= 1/x$ so that the density of $X$ is $$g(x)= {1\over\sqrt{\pi \log(1/x)}} e^{-(-\log(x))} (1/x) {\bf 1}_{(0,\infty)}(-\log(x)) = {1\over\sqrt{\pi \,\log(1/x)}}\, {\bf 1}_{(0,1)}(x).$$
Here is a graph of this function:
