Let $X = \{ 0,1,2 \}$ be a ternary alphabet and denote by $X^*$ the set of finite sequences (i.e. strings) with three symbols. For $w \in X^*$ with $n$ the length of $w$ and $w = w_1 w_2 \cdots w_n$ denote by $$\delta(w) = |\{ i \in \{ 2,\ldots, n \} : w_{i-1}w_i \in \{ 02, 20 \}\}|$$ the number of occurrence of $02$ or $20$ as substrings. For some fixed $n$ and $m$ how could we determine $$ \{ w \in X^n : \delta(w) \ge m \} $$ i.e. the set of length $n$ sequences such that the number of occurrences of $20$ or $02$ is greater than or equal to $m$? Also I am interested in the cardinality of this set, i.e. the number $|\{ w \in X^n : \delta(w) \ge m \}|$.
-
Hmm, you can do it in $O(nm)$ arithmetic operations by dynamic programming. Do you need to be faster than that? – hmakholm left over Monica Jul 27 '15 at 10:56
-
The definition of $\delta(w)$ begins with "For $w\in X^*$...". Shouldn't it say "For $x\in X^n...$"? And strings begin with $w_0$ or $w_1$? – ajotatxe Jul 27 '15 at 10:58
-
I am looking for a formula. Strings begin with $w_1$, I corrected the definition. – StefanH Jul 27 '15 at 11:13
-
I just realized that I assumed from the title that you were interested in the count, but the question actually says that you're interested in the set. Please resolve this discrepancy. – joriki Jul 27 '15 at 16:51
-
@joriki: Yes, sorry for the confusion... see my comment in the other thread http://math.stackexchange.com/questions/1375857/count-the-number-of-strings-containing-ac-or-ca-for-a-fixed-length-over-tern , maybe I should delete the other thread and put both questions in this thread.. – StefanH Jul 27 '15 at 17:49
-
Cool, thanks. No worries. – joriki Jul 27 '15 at 17:53
-
Unfornutely I cannot accept both answers... – StefanH Jul 27 '15 at 18:06
2 Answers
Here is a theoretical approach. I will slightly change your notation and take the alphabet $A = \{a,b,c\}$. Let us denote by $|u|_{ac}$ (respectively $|u|_{ca}$) the number of occurrences of the factor $ac$ (respectively $ca$) in $u$. Let $\delta: A^* \to \mathbb{N}$ the function defined by $\delta(u) = |u|_{ac} +|u|_{ca}$.
Step 1. Prove that $\delta$ is a sequential function and find a sequential transducer $\mathcal{A}$ that computes it. If I am not mistaken, this is one:
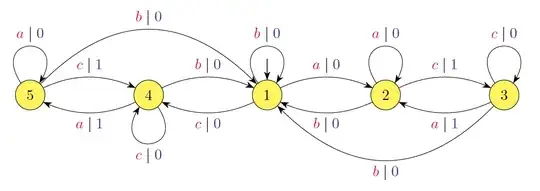
The vertical bar is a separator and $\delta(u)$ is obtained by adding the outputs when reading the word $u$, starting from the initial state. For instance, if $u = acacabcacacb$, you get $$1 \xrightarrow{a \mid 0} 2\xrightarrow{c \mid 1} 3 \xrightarrow{a \mid 1} 2 \xrightarrow{c \mid 1} 3\xrightarrow{a \mid 1} 2\xrightarrow{b \mid 0} 1 \xrightarrow{c \mid 0} 4 \xrightarrow{a \mid 1}5 \xrightarrow{c \mid 1} 4 \xrightarrow{a \mid 1} 5 \xrightarrow{c \mid 1} 4\xrightarrow{b \mid 0} 0$$ and thus $\delta(u) = 8$.
Step 2. Let $$ L_m = \delta^{-1}(\{m, m+1, \dotsm\}) = \{ u \in A^* \mid \delta(u) \geqslant m \} $$ Then $L_m$ is a regular language and an automaton accepting this language can be computed by taking the wreath product of $\mathcal{A}$ and of the minimal automaton of the language $a^ma^*$ on the alphabet $\{a\}$. The resulting automaton has $5 (m+1)$ states.
Step 3. (For the first version of your question, which has changed as I was writing this answer). Compute an unambiguous regular expression for $L_m$ (disjoint union, unambiguous product and unambiguous star) and then replace each letter of $A$ by $t$ to get the rational series $s = \sum_{n \in \mathbb{N}} |L_m \cap A^n| t^n$. Then use the Taylor expansion of $s$ in $0$ to get the value of $|L_m \cap A^n|$.
- 40,163
-
Great answer giving much insight. But Step 3 I did not get, I am not acquainted with the theory of rational series, so could you maybe provide some more details on how to derive a formula for $|L_m \cap A^n|$? – StefanH Jul 27 '15 at 16:33
-
Step 3 is no longer part of your question (you deleted it), and it requires some work to explain, so I would prefer if you were asking a separate question. – J.-E. Pin Jul 27 '15 at 16:55
-
Okay, yes I was not clear in formulating my question, here I reopened another thread: http://math.stackexchange.com/questions/1375857/count-the-number-of-strings-containing-ac-or-ca-for-a-fixed-length-over-tern – StefanH Jul 27 '15 at 17:32
-
-
@J.E.Pin: Okay, sorry for the mess, I edited the question, hoping now everything is clear and separated.. – StefanH Jul 27 '15 at 17:59
You can get a double sum using inclusion-exclusion. I doubt you'll find anything closer to a closed form than that.
Let $C$ be the set of $2(n-1)$ conditions of which we want the sequence to satisfy at least $m$, namely, the $n-1$ conditions that $02$ occurs at a certain position and the $n-1$ conditions that $20$ occurs at a certain position. Let $A_S$ with $S\subseteq C$ denote the set of sequences that satisfy all conditions in $S$. Then we want
$$ \left|\bigcup_{|S|=m}A_S\right|\;, $$
and by inclusion-exclusion this is
$$ \sum_{\scriptstyle S\subseteq C\atop\scriptstyle|S|\ge m}(-1)^{|S|-m}\binom{|S|-1}{m-1}\left|A_S\right|=\sum_{r=m}^n\sum_{\scriptstyle S\subseteq C\atop\scriptstyle|S|=r}(-1)^{r-m}\binom{r-1}{m-1}\left|A_S\right|\;, $$
where the right-hand side groups all sets $S$ with a certain number $|S|=r$ of restrictions together. These restrictions may overlap, but if $|A_S|$ is to be non-zero, they must overlap by at most $1$ per pair and be compatible, i.e. we cannot have $02$ and $20$ restrictions at the same position or $02$ and $02$ restrictions at successive positions, but we can have any number of blocks of alternating $02$ and $20$ restrictions. Let $k$ be the number of such blocks. Then $|A_S|=3^{n-r-k}$, since $n-r-k$ elements remain unrestricted. Thus, with $b_{rk}$ the number of ways to arrange $r$ restrictions in $k$ blocks, our sum is
$$ \sum_{r=m}^n\sum_{k=1}^n(-1)^{r-m}3^{n-r-k}\binom{r-1}{m-1}b_{rk}\;. $$
To determine $b_{rk}$, note that each block can start with either a $0$ or a $2$, for $2^k$ possibilities; we can distribute the $r$ restrictions over the $k$ blocks in $\binom{r-1}{k-1}$ ways; and we can select positions for the $k$ blocks among $n-r$ positions (of $k$ blocks and $n-r-k$ unrestricted entries) in $\binom{n-r}k$ ways. Putting it all together yields the desired count:
$$ \sum_{r=m}^n\sum_{k=1}^r(-1)^{r-m}2^k3^{n-r-k}\binom{r-1}{k-1}\binom{n-r}k\binom{r-1}{m-1} $$
(where binomial coefficients $\binom nk$ with $k\gt n$ are defined to be $0$ as usual).
Here's Java code that computes this double sum for arbitrary $m,n$.
P.S.: Stefan rightly pointed out in the comments that the inclusion-exclusion formula I used isn't the usual one and I should explain why it works.
Fix some sequence $w$. We want it to contribute $0$ to the sum if it fulfils less than $m$ conditions and $1$ otherwise. The first part is easy: If $w$ fulfils less than $m$ conditions, it isn't in any of the $A_S$ that appear in the sum.
So it remains to show that the contributions from $w$ add up to $1$ if it fulfils exactly a set $S'$ of $r'\ge m$ conditions. In this case $w$ contributes $1$ to every $|A_S|$ with $S\subseteq S'$, so the total contribution from $w$ is
\begin{eqnarray} &&\sum_{r=m}^n\sum_{\scriptstyle S\subseteq S'\atop\scriptstyle|S|=r}(-1)^{r-m}\binom{r-1}{m-1}\\ &=& \sum_{r=m}^{r'}(-1)^{r-m}\binom{r-1}{m-1}\binom{r'}r\\ &=& (-1)^{r'-m}\binom{-1}{m-1-r'}\\ &=&1\;, \end{eqnarray}
where I used the identity
$$ \sum_k\binom l{m+k}\binom{s+k}n(-1)^k=(-1)^{l+m}\binom{s-m}{n-k}\;, $$
which is proved on this very useful page using Vandermonde's convolution. (It's proved for non-negative $l$, $m$ and $s$, so we need to shift the index by $1$ to make the required $s$ non-negative.)
So every $w$ that we want to count contributes $1$ to the sum, which therefore yields the desired count.
P.P.S.: Here's a nicer, more combinatorial proof for the inclusion-exclusion formula for at least $m$ conditions (though in a roundabout way the other proof was also combinatorial in that Vandermonde's convolution has a nice combinatorial proof).
Let $l_r$ be the number of pairs $(S,w)$ such that $w$ fulfils all conditions in $S$ and $|S|=r$. That is, we count the number of sequences that fulfil at least $r$ conditions, but once for each set of $r$ conditions they fulfil. Let $e_r$ be the number of sequences that fulfil exactly $r$ conditions, and $d_r$ the number of sequences that fulfil at least $r$ conditions (where each sequence is now only counted once, not once per set of conditions fulfilled). Then
$$ e_i=\sum_{k=i}^n(-1)^{k-i}\binom kil_k\;. $$
(For some nice insights into this relationship, see this answer.) We want to show that
$$ d_i=\sum_{k=i}^n(-1)^{k-i}\binom {k-1}{i-1}l_k\;. $$
This fulfils the difference equation $e_i=d_i-d_{i+1}$, so by induction it's correct if it's correct for some $i$, which it is, since $e_n=d_n=l_n$.
(Full disclosure: I changed all the $\binom{r-1}{r-m}$ I had in the original post to $\binom{r-1}{m-1}$ because the proof made me realize that this is the more natural form; of course the two are equivalent.)
-
Guess the first formula should read $$ \left| \bigcup_{|S| \ge m} A_S \right|$$ ($\ge$ instead of $=$ in the index)? But staring at them your formulas seem rather mysterious to me... for example if we denote ${ S : |S| \ge m } = { S_1,\ldots, S_k }$, i.e. order the sets, then the principle of inclusion-exclusion says $$ \left| \bigcup_{|S| \ge m} A_S \right| = \sum_{ J \subseteq { 1,\ldots, k } , J \ne \emptyset } (-1)^{k+1} \left| \bigcap_{j \in J} A_{S_j} \right| $$ but I cannot relate that to your equations... – StefanH Jul 27 '15 at 18:36
-
@Stefan: On the first point: You seem to be reading $A_S$ as the set of sequences that satisfy exactly the conditions in $S$ (and no others). It is defined as the set of sequences that satisfy all conditions in $S$ (and possibly also others). Then we don't need $\ge$, since $A_S'\subseteq A_S$ if $S\subseteq S'$. I'm not sure whether your second point will remain open when you take this into account; if it does, feel free to write again. – joriki Jul 27 '15 at 18:43
-
Okay, but even if the union is taken over the sets such that $|S| = m$ and I order them $S_1, \ldots, S_k$ and write the formula for inclusion-exclusion as in my previous comment I do not see how to get your formula which looks a little strange to me... – StefanH Jul 27 '15 at 18:52
-
@Stefan: You're right, I should have explained that formula. I appended an explanation to the answer. – joriki Jul 27 '15 at 20:16
-
@Stefan: I added another, nicer proof for the inclusion-exclusion formula. Thanks, by the way; I was always using this formula but never really thought about it properly before you forced me to :-) That cleared things up a bit for me, too. – joriki Jul 27 '15 at 22:54