How many different sums of parts of a vector

Question

The following mathematical puzzle was given to me by a friend a while ago and I can't work out how to solve it. Does anyone have any ideas?

For a given vector $v \in \{-1,1\}^n$ we consider the following $n$ sums. $$S_j=\sum_{i=0}^j v_i - \sum_{i=j+1}^{n-1} v_i \text{ for } 0 \leq j \leq n-1.$$

For example if $v = (-1,1,1)$ then $S=(-3,-1,1).$

Now let $T_j = 1$ if $S_j>0$ and $0$ otherwise. So for our example vector $v$ we have that $T=(0,0,1)$

Considered over all $2^n$ possible vectors $v$, the question is how many different possible vectors $T$ are there?

I think if $n=2$ the answer is $3$, if $n=3$ the answer is $8$, if $n=4$ the answer is $11$, if $n=5$, the answer is $22$ and if $n=6$ the answer is $31$.

---

Posted to https://mathoverflow.net/questions/212389/how-many-different-sums-of-parts-of-a-vector where a possible answer has been given in the comments.

Answer 1

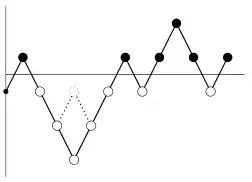
Let $t_n$ be the number of distinct vectors $T$ of length $n$ that can be made using the above process. Here I will just provide an upper bound on $t_n$. That is $t_n \leq 2F_{n + 2}$, where $F_n$ is the $n^{th}$ Fibonnaci number. First, some definitions; then a proof.

Definition (Compressed form): For any vector $U$ whose elements are in $\{0, 1\}$, we can write it it's compressed form $C$ as follows: $u_0[c_1, c_2, \dots, c_m]$. Here $u_0$ is the initial term, and each $c_i$ is a non-zero natural number representing a contiguous run of $0$ or $1$. Note in particular that $m \leq n$ always holds. For example, the sequence $(0, 1, 1, 1, 0, 0, 1)$ would be represented as $0[1, 3, 2, 1]$.

Proof (of upper bound): Well, according to the lemma below, we know that the compressed form $C$ of any vector $T$ can only have $c_i$ terms are all odd, except possibly the first and last terms. Also, no term is $0$. It is also clear that the sum $c_1 + c_2 + \dots + c_m = n$, from the definition of a compressed sequence. From elsewhere, we can show that the number of odd sequences adding up to some number $n$ is $F_{n + 2}$. Now, if we relax this constraint so that the first and/or last term can be even, we get four possibilities for the first/last term: even/even, even/odd, odd/even, odd/odd. Subtracting 1 from a non-zero even number always gives us an odd number, so the above number of combinations above are $F_{n - 2}, F{n - 1}, F{n - 1}, F_{n}$. Summing these up and using the standard Fibonnaci recurrence gives $F_{n + 2}$. Now, the first term of a compressed sequence can be either $1$ or $0$, so we get $2F_{n + 2}$ for an upper bound, as required.

Lemma: The compressed form of any vector $T$, constructed as in the question, contains all odd numbers, except at its first and last terms. To see why this is the case, consider some intermediate term $k$ in the compressed form. This corresponds to a run $T_{i + 1}, T_{i + 2}, \dots, T_{i + k}$, with $T_{i + k + 1} = T_{i} \neq T_{i + 1}$ and $T_{i + j} = T_{i + h}$ for all $1 \leq j, h \leq k$. That is, it corresponds to $k$ a sub-sequence of $k$ equal terms in a row, and two different terms immediately before and after the sequence, which are themselves equal. Now, suppose $k$ is even, towards a contradiction. Well, consider the $S$ vector that created the $T$ vector. Notice that for any $a$, $S_{a + 1} = S{a} \pm2$. Also note that $T_i \neq T_{i + 1}$ by definition. Now define $D_a = \frac{S_{i + a} - Si}{2}$. We show, inductively, that for odd $a$, this value is odd, and for even $a$ it is even. This is clearly true for $a = 0$. For the inductive case $a = n + 1$, we know that $S_{n + 1} = S_{n}\pm2$. So $D_{n + 1} = D_n\pm1$. So the parity of $D_n$ clearly alternates between successive terms. Now, we have assumed an even $k$. Which means $D_k$ must be even, and $D_{k + 1}$ odd. So then $S_{i + k + 1} \neq S_i$. But by the definition of the compressed form, $T_{i + k + 1} = T_i$. The only way this is possible, from the definition of $T$, is if $S_{i + k + 1} = S_{i} - 2$ and $S_i \leq 0$ or $S_{i + k + 1} = S_{i} + 2$ and $S_i > 0$. But both of these cases imply that $T_{i + k} = T_{i + k + 1}$, which is a contradiction, so $k$ cannot be even.

---

Lemma (*): For $u \in \{0, 1\}$ every vector, which in compressed form is written $u[1, 1, \dots, 1]$, is constructable with the above process. To proves this, consider first the case of $u = 0$. Then we can see that the vector $V = (1, -1, 1, -1, \dots)$ results in a vector $T = (0, 1, 0, 1, \dots)$. This is because the associated vector $S$ will be either $(0, 2, 0, 2, \dots)$ or $(-1, 1, -1, 1, \dots)$, depending on the parity of the length. For the case of $u = 1$, the vector $V = (-1, 1, -1, 1, \dots, -1, -1)$ or $V = (-1, 1, -1, 1, \dots, -1)$ will work. This is because the associated $S$ vector will be either $(2, 0, 2, 0, \dots)$ or $(1, -1, 1, -1, \dots)$, again depending on parity of length.

Lemma (**): All vectors in compressed form $C = u[c_1, c_2, \dots, c_m]$ are constructible with the above process whenever all $c_i$ are odd. We prove this by induction on $n$, the length of the original vector $V$. We start with two base cases $n = 1, 2$, so that we can jump by two in the inductive case. Well, we notice that both case we get that all $c_i$ being odd implies all $c_i = 1$, and so by (*) we are done.

For the inductive case, again if all $c_i = 1$, then we can just apply (*) and we're done. Else there is some $c_i \geq 3$. But then by induction the compressed form $u[c_1, c_2, \dots, c_i - 2, \dots, c_m]$ can be constructed. Now, look at the associated vector $T$ that results in this compressed form. The term $c_i - 2$ in the compressed vector corresponds to either $c_i - 2$ $0$s or that many $1s$ in a row. In either case, we can extend this to $c_i$ $0$s or $1$s by adding $(-1, 1)$ or $(1, -1)$ at the corresponding slot in the corresponding vector $V$. Doing this preserves the other $c_i$, and so we achieve our desired $C$.

Corollary (lower bound): A lower bound for $t_n$ is $2F_n$. That is $2F_n \leq t_n$. This is because the number of vectors of odd numbers adding up to $n$ is $F_n$ (as shown elsewhere), and the start term in the compressed form can be either $0$ or $1$.

---

Putting it all together, we have: $2F_n \leq t_n \leq 2F_{n + 2}$.

Answer 2

Let $w=\sum_i v_i$ be the weight of $v$. The vector $S$ can be interpreted as a walk from $(0,-w)$ to $(n,w)$ with steps $(1,\pm2)$, in which the start point is not recorded. The $T$ vector records whether the $y$ coordinate of the path is positive or not.

For example, the following figure illustrates the path for $v=(+---+++-++--+)$ whose $T$ vector is $1000001011101$, which we abbreviate as $1[1511311]$, recording the first term and the lengths of the runs.

$\qquad\qquad\qquad\qquad\qquad\qquad$

If a path strays above $4$ or below $-3$, then there's another path with the same $T$ vector that doesn't (as illustrated by the dotted line in the figure), so we can restrict our analysis to vectors whose weight is in the interval $[-3,4]$.

For each of these weights, the possible sequences of numbers in the abbreviated form of the $T$ vector are as follows. We use $\textsf{e}$ to denote an even number, $\textsf{o}$ to denote an odd number, and $(\textsf{oo})^\star$ to denote a sequence of zero or more pairs of odd numbers. $$ \begin{array}{llll} w = \phantom{-}4 : & 0[\textsf{e}(\textsf{oo})^\star \textsf{e}] \\[3pt] w = \phantom{-}3 : & 0[\textsf{o}(\textsf{oo})^\star \textsf{e}] \\[3pt] w = \phantom{-}2 : & 0[\textsf{o}(\textsf{oo})^\star \textsf{o}] \\[3pt] w = \phantom{-}1 : & 0[\textsf{e}(\textsf{oo})^\star \textsf{o}] & \quad\text{or}\quad 1[\textsf{oo}(\textsf{oo})^\star \textsf{o}] & \quad\text{or}\quad 1[\textsf{o}] \\[3pt] w = \phantom{-}0 : & 1[\textsf{o}(\textsf{oo})^\star \textsf{o}] & \quad\text{or}\quad 0[\textsf{eo}(\textsf{oo})^\star \textsf{o}] & \quad\text{or}\quad 0[\textsf{e}] \\[3pt] w = -1 : & 1[\textsf{e}(\textsf{oo})^\star \textsf{o}] & \quad\text{or}\quad 0[\textsf{oo}(\textsf{oo})^\star \textsf{o}] & \quad\text{or}\quad 0[\textsf{o}] \\[3pt] w = -2 : & 1[\textsf{e}(\textsf{oo})^\star \textsf{e}] & \quad\text{or}\quad 0[\textsf{oo}(\textsf{oo})^\star \textsf{e}] & \quad\text{or}\quad 0[\textsf{e}] \\[3pt] w = -3 : & 1[\textsf{o}(\textsf{oo})^\star \textsf{e}] \end{array} $$ These sets of $T$ vectors are disjoint except for the two identical terms in the last column.

To enumerate, we use generating functions, remembering that the numbers in the abbreviated forms represent runs in the $T$ vectors.

Let $s(z)=1/(1-z)$ and $r(z)=zs(z)$ be the generating functions for possibly empty sequences and nonempty runs respectively. Then $e(z)=r(z^2)$ and $o(z)=zs(z^2)$ are the generating functions for nonempty even and odd length runs respectively. The generating function for the number of distinct $T$ vectors is thus $$ 2r(z)^2s(o(z)^2) \:+\: 2r(z)o(z)^2s(o(z)^2) \:+\: r(z)+o(z) \;=\; \frac{2z+3z^2-z^4-2z^5-z^6}{1-4z^2+4z^4-z^6} , $$ where the first two summands come from the first and second columns in the table, noting that $e(z)+o(z)=r(z)$.

This generating function is the same as that ‘guessed’ by Jay Pantone on MathOverflow.

Extracting coefficients gives the number of distinct $T$ vectors of length $n$; one way of expressing this is $$ t_n \;=\; \left\{ \begin{array}{ll} 4f_n - 1, & n\;\text{even}, \\[3pt] 2f_n + 4f_{n-1}, & n\;\text{odd}, \end{array} \right. $$ where $f_n$ is the $n$th Fibonacci number ($f_0=0$, $f_1=1$).