Cubic Planar Graphs have $2^m-1$ Hamilton Cycles, contradicting Bosak...

Question

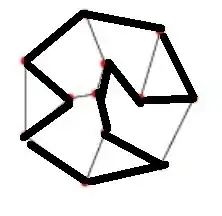
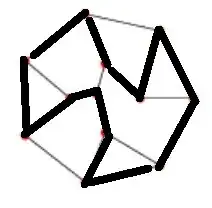
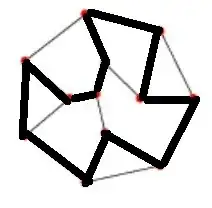
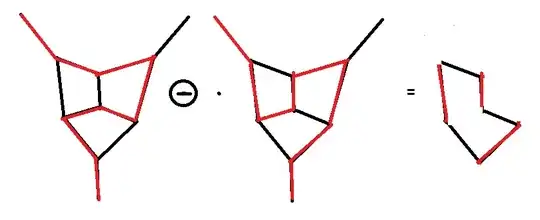
I looked at the symmetric difference of hamilton cycle (HC) in cubic planar graphs and found that, together with the empty graph, they build a subgroup of the abelian group $\Omega$ of symmetric differences of cycles. This is easily illustrated by the HCs of Frucht graph:

Check yourself that the symmetric difference of any pair gives the third HC! (Also interesting to note that the set of cuts of pairs builds a $3$-edge coloring of the graph!)

Now the cycle space is spanned by the faces $f_k\in F$ of $G$ and is kind of a power set of faces, since in the total symmetric sum, you turn on/off a certain face. This results in a $F$ dimensional vector space over $\mathbb Z_2$, which has $2^F$ elements, which are the group elements of $\Omega$.

Now I wonder if it is true in general, that the number of HCs plus $1$ divides $2^F$, since the subgroup is normal, even central. As shown in a reference here we will always have three HCs in cubic graphs.

Fine, but this opposes what I read somewhere else (trying to provide a reference) that bicubic graphs always have four HCs. Or don't these four build a single subgroup, but rather a set of subgroups?

What happens in the bicubic case and is it true for cubic ones that they always have $2^m-1$ HCs?

I'm confused, since I found this quote "Every cubic bipartite graph has an even number of Hamilton cycles." from J. Bosak, Hamiltonian lines in cubic graphs,Theory of Graphs, International Symposium, Rome, July 1966 , Gordon & Breach, New York, (1967), 35–46. for example here, contradicting my assumption...

Answer 1

Let $K$ be the aforementioned group of Hamiltonian cycles. It has size $H+1$, where $H$ is the number of Hamiltonian cycles.

Let $J$ be the group of $S\subset \mathscr{P}(\text{faces})$ under symmetric difference.

I'll formalise your idea about each Hamiltonian cycle $h$ being sent to a set $f(h)$ of faces monomorphically by $f:J \to K$, then, noting that $\vert\text{im}f\vert \mid \vert K\vert=2^n$, we're done.

It's reasonably clear that a cycle is Hamltonian if its interior is a $2$-vertex connected set whose boundary contains all vertices (call the set of these $J'$). Thus there is a bijection sending cycles $h$ to $j_h\in J' \subset J$. Define $f$ using this. It's mostly obvious that $f$ is a homomorphism.

All that remains to check is that, if $h,g$ are Hamiltonian cycles, $f(hg)$ is the expected element in $J$: $f(h) \Delta f(g)$. Indeed, consider $f(h) \Delta f(g)$, which corresponds to some Hamiltonian cycle by the above paragraph.

To show that this is $f(gh)$, look locally at each vertex $v$. For simplicity $h \ne g$ at this vertex. Then two of the three edges of $v$ are transversed by $g$ and $h$, not both the same for $g$ and $h$. Taking the symmetric difference gives two new edges. With a couple of casebashes it's obvious that these two new edges are the boundary of $f(g)\Delta f(h)$ near $v$.

If $h,g$ agree near $v$ it's trivial.

TL;DR: The map taking a HC to the set of faces it encloses is monomorphic, then look at cardinalities.

Answer 2

Morgan was right: I haven't checked simple counter examples. Here is one. A graph might contain 3 adjacent squares, which gives rise for two kinds of hamiltonian cycles and the symmetric difference is not another HC, but a seperated cycle.