2

We have the following argument:
$P \implies Q$ (Premise 1)
$P$ (Premise 2)
$—$
$∴Q$ (Conclusion)

The accompanying truth table is:

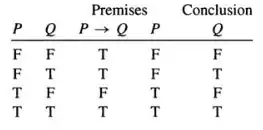
enter image description here

I don't understand this section of my textbook:

The premises are both true only in line four of the table, and in this line the conclusion is true as well.

You can also see from the truth table that both premises are needed to make this argument valid. But if we were to change the truth table for the conditional statement to make P → Q false in the first line of the table, then the second premise of this argument would no longer be needed.

We would end up with the conclusion that, just from the single premise P → Q, we could infer that Q must be true, since in the two lines of the truth table in which the premise P → Q would still be true, lines two and four, the conclusion Q is true too.

My thinking:

If we would change the $P → Q$ to be false in the first line of the truth table. Then why couldn't the conclusion be false as well? I don't understand what line $2$ and $4$ have anything to do with line $1$?

Lukas Arvidsson
  • 2,376

2 Answers2

1

The discussion is about why the statement $\bot \to \bot$ is considered "true" rather than "false".   That is, why the truth table of the conditional connective is defined as it is.

An argument is considered valid if, it guarantees the conclusion is true when all the premises are true.

So if $\to$ is defined as it is, then the truth of both premises, $\{P\to Q, P\}$ are required to guarantee the truth of the conclusion $Q$.   (Knowing only that one is true is not enough to ensure the conclusion is true.)

$$\begin{array}{cc|cc|cc}P & Q & P\to Q & P & Q \\ \hline \bot & \bot & \top & \bot & \bot \\ \bot & \top & \top & \bot & \top \\ \top & \bot & \bot & \top & \bot \\ \top & \top & \top & \top & \top & \star \end{array}$$

However if we defined $\dot\to$ so that $\bot \dot\to \bot = \bot$ we only need the one premise $P\dot\to Q$ to guarantee the conclusion. The conclusion is always true when that premise is, whatever $P$ may be.

$$\begin{array}{cc|c|cc}P & Q & P\dot\to Q & Q \\ \hline \bot & \bot & \bot & \bot \\ \bot & \top & \top & \top & \star \\ \top & \bot & \bot & \bot \\ \top & \top & \top & \top & \star \end{array}$$

Graham Kemp
  • 129,094
0

As I understand your textbook:

If $(P\rightarrow Q)$ True and $P$ False then Q is False, which is true.

And if I didn't make errors (I just did it by head) others are right.

NB: If you need examples I can give you one for each ! ;)

ParaH2
  • 1,672
  • Thanks for your answer! This is not how I understand the question. To me they are saying that if we make $P \implies Q$ false, the we don't need to look at $P$ and we can see that $Q$ is true by looking at line $2$ and $4$... I don't understand the logic in this... – Lukas Arvidsson Jul 20 '15 at 23:57
  • I don't understand what you don't understand sorry. – ParaH2 Jul 21 '15 at 00:00