Newton's method $x−x^3=0$

Question

1. Find a positive initial guess $x_0$ for the positive zero of $x−x^3=0$ for which Newton's method gives an undefined quantity for $x_1$.

2. Find a positive initial guess x0 for the zero of $x−x^3=0$ for which Newton's method bounces back and forth infinitely. (Use symmetry.)

3. Find the largest interval around each of the roots $x−x^3=0$ such that Newton's method converges to that root for every initial guess $x_0$ in that interval. (Use your previous two answers here.)
   Interval converging to $x=−1$
   Interval converging to $x=0$
   Interval converging to $x=1$

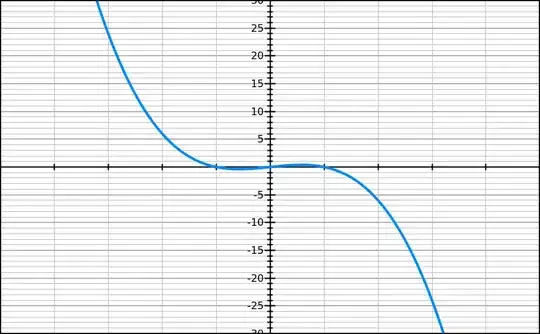
so, my graph will look like that. (x is between -5 and 5)
I don't really know how to start. If i get $x_0$ as $1$ or $0$ I will get the same result for every $x$ with Newton's method. Cause this numbers are my roots, what should i take as $x_0$, if I already know the roots. I can't get it.
thanks in advance.

Answer 1

See How to solve for the interval of convergence in Newton's Method? for details on convergence intevals.

Graphically it helps to visualize Newton's method as drawing a tangent to the curve at the $x_n$. Then $x_{n+1}$ is where the tangent intersects the x-axis. Your steps 1 and 2 identified two ways that the method can fail, namely when the slope of the tangent is zero and never intersects the x-axis, and where $x_n$ and $x_{n+1}$ oscillate back and forth.

For step 3 your graph shows that for $x_n < -1$ the tangent line will move $x_{n+1}$ closer to the root $-1$ The same is true for $x_n > -1$ until we hit the local minimum (i.e. flat slope) of the curve found in step 1. So the Interval converging to $x=−1$ will be at least $(-\infty,-\sqrt\frac1{3})$ and the interval converging to $x=1$ is symmetric.

The Interval converging to $x=0$ is limited by the failure points found in step 2: $(-\sqrt\frac1{5},\sqrt\frac1{5})$. Note how the slope here points towards the root $0$.

So what about $(-\sqrt\frac1{3},-\sqrt\frac1{5})$ and the symmetric $(\sqrt\frac1{5},\sqrt\frac1{3})$? These appear to be chaotic regions. -0.45 converges to $-1$, -0.46 converges to $1$. The method overshoots with $x_n$ bouncing back and forth between positive and negative values until $|x_n|>1$ and it then converges to either $1$ or $-1$. These intervals fail to have a single value of convergence.

Answer 2

For (1), think about a local max. Newton's method involves dividing by the slope at $ x_n $, so how could this be problematic?