I've found two different methods to prove Internal Angle Bisector Theorem, viz. Wikipedia ("Proof 2") method and AskMath.com method.
How can we prove External Angle Bisector Theorem with Wikipedia's "Proof 2" method, in which they draw perpendiculars on the angle bisector?
My effort:
I tried to draw a perpendicular upon the external bisector from the two vertices of the triangle, but I couldn't find the similar triangles as in Proof 2 of Wikipedia.
Consider the following:
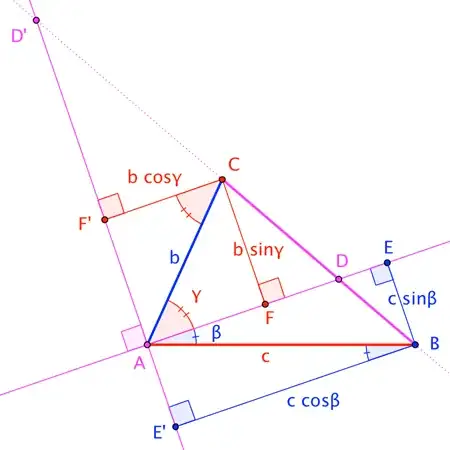
Here, points $D$ and $D^\prime$ are on the (extended) side $\overline{BC}$ of $\triangle ABC$, such that $\angle DAD^\prime$ is a right angle. (If one of $D$ and $D^\prime$ is the foot of the altitude from $A$, then we may take the other to be the "point at infinity" on $\overleftrightarrow{BC}$, so that the line joining it to $A$ is parallel to $\overleftrightarrow{BC}$.) We'll take each of the marked angles $\beta$ and $\gamma$ to be non-obtuse; the reader is invited to adjust this argument for the obtuse case.
Dropping perpendiculars from $B$ and $C$ to respective points $E$ and $F$ on $\overleftrightarrow{AD}$, and to respective points $E^\prime$ and $F^\prime$ on $\overleftrightarrow{AD^\prime}$, we have (for finite $D$) $$\triangle BED \sim \triangle CFD \qquad\implies\qquad \frac{|\overline{BD}|}{|\overline{CD}|} = \frac{|\overline{BE}|}{|\overline{CF}|} = \frac{c \sin\beta}{b \sin\gamma} \tag{$\star$}$$ and (for finite $D^\prime$) $$\triangle BE^\prime D^\prime \sim \triangle CF^\prime D^\prime \qquad\implies\qquad \frac{|\overline{BD^\prime}|}{|\overline{CD^\prime}|} = \frac{|\overline{BE^\prime}|}{|\overline{CF^\prime}|} = \frac{c \cos\beta}{b \cos\gamma} \tag{$\star\star$}$$
(These results effectively constitute internal and external versions of what the Wikipedia article terms the "generalized angle bisector theorem", generalizing "angle bisector" to a line that may-or-may-not actually bisect the angle. Be that as it may ...)
If one of $\overleftrightarrow{AD}$ and $\overleftrightarrow{AD^\prime}$ is an (interior or exterior) angle bisector, then the other is necessarily an (exterior or interior) angle bisector. In such a case, $\beta = \gamma$, and the trigonometric factors cancel in $(\star)$ and $(\star\star)$, leaving the Internal/External Angle Bisector Theorem $$\frac{|\overline{BD}|}{|\overline{CD}|} = \frac{c}{b} = \frac{|\overline{BD^\prime}|}{|\overline{CD^\prime}|}$$