Calculating a real integral using complex integration

Question

$$\int^\infty_0 \frac{dx}{x^6 + 1}$$

Does someone know how to calculate this integral using complex integrals? I don't know how to deal with the $x^6$ in the denominator.

Answer 1

Thankfully the integrand is even, so we have

$$ \int^\infty_0 \frac{dx}{x^6 + 1} = \frac{1}{2}\int^\infty_{-\infty} \frac{dx}{x^6 + 1}. \tag{1} $$

To find this, we will calculate the integral

$$ \int_{\Gamma_R} \frac{dz}{z^6+1}, $$

where $\Gamma_R$ is the semicircle of radius $R$ in the upper half-plane, $C_R$, together with the line segment between $z=-R$ and $z=R$ on the real axis.

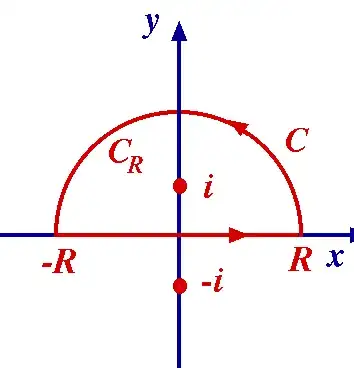
(Image courtesy of Paul Scott.)

Then

$$ \int_{\Gamma_R} \frac{dz}{z^6+1} = \int_{-R}^{R} \frac{dx}{x^6+1} + \int_{C_R} \frac{dz}{z^6+1}. $$

We need to show that the integral over $C_R$ vanishes as $R \to \infty$. Indeed, the triangle inequality gives

$$\begin{align} \left| \int_{C_R} \frac{dz}{z^6+1} \right| &\leq L(C_R) \cdot \max_{C_R} \left| \frac{1}{z^6+1} \right| \\ &\leq \frac{\pi R}{R^6 - 1}, \end{align}$$

where $L(C_R)$ is the length of $C_R$. From this we may conclude that

$$ \lim_{R \to \infty} \int_{\Gamma_R} \frac{dz}{z^6+1} = \int_{-\infty}^{\infty} \frac{dx}{x^6+1}. \tag{2} $$

The integral on the left is evaluated by the residue theorem. For $R > 1$ we have

$$ \int_{\Gamma_R} \frac{dz}{z^6+1} = 2\pi i \sum_{k=0}^{2} \operatorname{Res}\left(\frac{1}{z^6+1},\zeta^k \omega\right), $$

where $\zeta$ is the primitive sixth root of unity and $\omega = e^{i\pi/6}$. Note that this is because $\omega$, $\zeta\omega$, and $\zeta^2 \omega$ are the only poles of the integrand inside $\Gamma_R$. The sum of the residues can be calculated directly, and we find that

$$ \int_{\Gamma_R} \frac{dz}{z^6+1} = 2\pi i \sum_{k=0}^{2} \operatorname{Res}\left(\frac{1}{z^6+1},\zeta^k \omega\right) = \frac{\pi}{3 \sin(\pi/6)} = \frac{2\pi}{3}. $$

Thus, from $(1)$ and $(2)$ we conclude that

$$ \int_{0}^{\infty} \frac{dx}{x^6+1} = \frac{\pi}{3}. $$

In general,

$$ \int_{0}^{\infty} \frac{dx}{x^{2n}+1} = \frac{\pi}{2 n \sin\left(\frac{\pi}{2n}\right)} $$

for $n \geq 1$.

Answer 2

$$\int_0^\infty\frac{dx}{x^6+1}=\frac{1}{2}\lim_{R\to\infty}I_R$$ where $$I_R:=\int_{-R}^{R}\frac{dx}{x^6+1}.$$ Let us integrate $f(z):=\frac{1}{1+z6}$ along the closed oriented curve constituted by the upper semicircumpherence $C_R$ with center $0$ and radius $R>1$ and the interval $[-R,R]$.

Applying the residue theorem we get $$I_R+\int_{C_R}f(z)dz=2\pi i\sum_{k=1}^3\textrm{Res}(f;\textrm{exp}(\frac{1+2k}{6}i\pi)).\qquad(*)$$

Remarking $\lim_{R\to\infty}\int_{C_R}f(z)dz=0,$ from $(*)$ you get your integral.

Answer 3

You can split the denominator by taking $x^6$ as $(x^2)^3$, and then use $a^3+b^3=(a+b)(a^2-ab+b^2)$. After using this formula, you will get $x^6+1=(x^2+1)(x^4-x^2+1)$. Then you can use partial fraction decomposition.

If you still don't get it, then here is another better method in this little video.