1

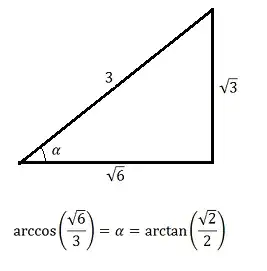
I get the following results after solving the equation $\sqrt[4]{1 - \frac{4}{3}\cos(2x) - \sin^4(x)} = -\,\cos(x)$, : $$ x_{1} = \pi - \arccos(\frac{\sqrt{6}}{3}) + 2\pi n: n \in \mathbb{Z}\\ x_{2} = \pi + \arccos(\frac{\sqrt{6}}{3}) + 2\pi n: n \in \mathbb{Z} $$

Wolfram Alpha, here the link, instead, gives the following results:

$ x_{1} = 2\pi n - 2\arctan(\sqrt{5 + 2\sqrt{6}}) : n \in \mathbb{Z}\\ x_{2} = 2\pi n + 2\arctan(\sqrt{5 + 2\sqrt{6}}) : n \in \mathbb{Z} $

Now, supposing that my solutions are correct, this means that there must be a relation between:

$\pi - \arccos(\frac{\sqrt{6}}{3})$ and $- 2\arctan(\sqrt{5 + 2\sqrt{6}})$

or between:

$\pi + \arccos(\frac{\sqrt{6}}{3})$ and $+ 2\arctan(\sqrt{5 + 2\sqrt{6}})$

or viceversa. But, given the solutions I have found, how can I prove that they are effectively the same as the solutions Wolfram found? Mathematically?

P.S.: I have found out, by looking at the graphs of $y_{1} = \pi - \arccos(\frac{\sqrt{6}}{3})$ and $y_{2} = 2\arctan(\sqrt{5 + 2\sqrt{6}})$ e.g., that:

$\pi - \arccos(\frac{\sqrt{6}}{3}) = 2\arctan(\sqrt{5 + 2\sqrt{6}})$

Then, of course: $\pi - \arccos(\frac{\sqrt{6}}{3}) + 2\pi = 2\arctan(\sqrt{5 + 2\sqrt{6}})+ 2\pi \\ \pi - \arccos(\frac{\sqrt{6}}{3}) + 4\pi = 2\arctan(\sqrt{5 + 2\sqrt{6}})+ 4\pi \\ ... every\,\,360°n, n \in \mathbb{Z}$

And that:

$\pi + \arccos(\frac{\sqrt{6}}{3}) = -2\arctan(\sqrt{5 + 2\sqrt{6}})+ 2\pi\\ \pi + \arccos(\frac{\sqrt{6}}{3}) + 2\pi = -2\arctan(\sqrt{5 + 2\sqrt{6}})+ 4\pi\\ \pi + \arccos(\frac{\sqrt{6}}{3}) + 4\pi = -2\arctan(\sqrt{5 + 2\sqrt{6}})+ 6\pi\\ ... \pi + \arccos(\frac{\sqrt{6}}{3}) + (n - 2)\pi = -2\arctan(\sqrt{5 + 2\sqrt{6}})+ n\pi\\ $

So we can say that $\pi + \arccos(\frac{\sqrt{6}}{3}) + (n - 2)\pi$ differs from $-2\arctan(\sqrt{5 + 2\sqrt{6}}) + n\pi$ by just one lap ($2\pi$), otherwise they can be safely considered the same (for all integers).

So how to rewrite $\arccos$ in terms of $\arctan$?

Thanks for the attention!

Paolo
  • 935
user3019105
  • 499
  • 2
    The downvote seems harsh, I am of the opinion that the OP has gone to some thorough effort with his question. – Autolatry Jul 09 '15 at 14:18

3 Answers3

1

We define $y = \arccos \left( \dfrac{\sqrt{6}}{3} \right)$. Since $0 < \dfrac{\sqrt{6}}{3} < 1$, we have $0 < y < \dfrac{\pi}{2}$, and $\dfrac{\pi}{2} < \pi - y < \pi$. Therefore, \begin{equation*} \tan \left( \frac{\pi - y}{2} \right) = \sqrt{\frac{1 - \cos (\pi - y)}{1 + \cos (\pi + y)}} = \sqrt{\frac{1 + \cos y}{1 - \cos y}} = \sqrt{\dfrac{1 + \frac{\sqrt{6}}{3}}{1 - \frac{\sqrt{6}}{3}}} = \sqrt{\frac{3 + \sqrt{6}}{3 - \sqrt{6}}} = \sqrt{5 + 2\sqrt{6}}. \end{equation*} Then we have \begin{equation*} \pi - y = 2 \arctan \left( \sqrt{5 + 2\sqrt{6}} \right), \end{equation*} that is \begin{equation*} \pi - \arccos \left( \frac{\sqrt{6}}{3} \right) = 2 \arctan \left( \sqrt{5 + 2\sqrt{6}} \right), \end{equation*} By the same token, we have $\pi < \pi + y < \dfrac{3}{2} \pi$. Therefore, \begin{equation*} \begin{split} \tan \left( \frac{\pi + y}{2} \right) &= -\sqrt{\frac{1 - \cos (\pi - y)}{1 + \cos (\pi + y)}} = -\sqrt{\frac{1 + \cos y}{1 - \cos y}} \\ &= -\sqrt{\dfrac{1 + \frac{\sqrt{6}}{3}}{1 - \frac{\sqrt{6}}{3}}} = -\sqrt{\frac{3 + \sqrt{6}}{3 - \sqrt{6}}} = -\sqrt{5 + 2\sqrt{6}}. \end{split} \end{equation*} Then we have \begin{equation*} \pi + y = 2 \arctan \left( -\sqrt{5 + 2\sqrt{6}} \right) = -2\arctan \left( \sqrt{5 + 2\sqrt{6}} \right), \end{equation*} that is \begin{equation*} \pi + \arccos \left( \frac{\sqrt{6}}{3} \right) = -2 \arctan \left( \sqrt{5 + 2\sqrt{6}} \right). \end{equation*} From this exercise, you can easily prove a general trigonometric relation between $\arccos$ and $\arctan$.

Paolo
  • 935
  • Nice proof! But you made a mistake: when you prove that $\pi - y = 2\arctan(\sqrt{5 + 2\sqrt{6}})$, you say $\frac{\pi}{2} < y < \pi$ and $0 < \pi - y < \frac{\pi}{2}$, but as $0 < \frac{\sqrt{6}}{3} < 1$ and $\arccos(a)$'s codomain is $[0, \pi]$, $y = \arccos(\frac{\sqrt{6}}{3})$ must be $0 < y < \frac{\pi}{2}$ and $\frac{\pi}{2} < \pi - y < \pi$ and therefore $\frac{\pi}{4} < \frac{\pi - y}{2} < \frac{\pi}{2}$, hence the positive tangent.For the second proof, $\frac{\pi}{2}< \frac{\pi + y}{2} < \frac{3\pi}{4}$, hence the negative $tan$. $\frac{3}{2}\pi< y < 2\pi$ is wrong, what do you think? – user3019105 Jul 09 '15 at 17:35
  • Yes, you're right. I'm sorry for the mistake. I'll edit right away. Thanks. – Paolo Jul 09 '15 at 18:06
  • But I think that in the second part the negative $\tan$ is correct for the exact reason you say: $\frac{\pi}{2} < \frac{\pi + y}{2} < \frac{3}{4}\pi$. In that interval $\tan$ is negative. Am I wrong? – Paolo Jul 09 '15 at 18:15
  • Yes, you're right, tan is negative because between $\frac{\pi}{2}$ and $\frac{3}{4}\pi$ you are in Quadrant II, where cosine is negative. Anyway, thanks for having shown why and how $\arccos(x)$ equals $2 \arctan(y)$! – user3019105 Jul 09 '15 at 20:27
1

Let $\arctan x=y\implies x=\tan y$

Using this, $0\le y\le\dfrac\pi2\iff0\le2y\le\pi$ and $\arccos$ lies in $[0,\pi]$

$\cos2y=\dfrac{1-\tan^2y}{1+\tan^2y}=\dfrac{1-x^2}{1+x^2}$

$\implies\arccos\dfrac{1-x^2}{1+x^2}=2y=2\arctan x$ if $0\le2\arctan x\le\pi\iff0\le\arctan x\le\dfrac\pi2\implies0\le x\le\infty$

For $x<0\implies-\dfrac\pi2\le\arctan x<0\implies-\pi\le2y<0\iff0<-2y\le\pi$

As $\cos(2y)=\cos(-2y),$

$\implies\arccos\dfrac{1-x^2}{1+x^2}=-2y=-2\arctan x$

$\iff2\arctan x=-\arccos\dfrac{1-x^2}{1+x^2}$ if $x<0$

See also, How do I prove that $\arccos(x) + \arccos(-x)=\pi$ when $x \in [-1,1]$?

Community
  • 1
lab bhattacharjee
  • 274,582
0

You can see in the figure the angle $\alpha$ corresponding to $\arccos(\frac{\sqrt{6}}{3})$ and the tangent of the same $\alpha$ from which you can easily deduce your own conclusion.

enter image description here

Piquito
  • 29,594
  • I am sorry, I didn't get your explanation, I know that $\arccos \frac{\sqrt{6}}{3} = \alpha = \arctan \frac{\sqrt{2}}{2}$, but why the triangle with a $cos(\alpha) = \sqrt{6}$ if $arccos$ is for the value $\frac{\sqrt{6}}{3}$ of the cosine? – user3019105 Jul 09 '15 at 17:44