3

I want to find ellipse circumference using 5 points. I have 5 point of an arc of the ellipse. To reach my goal i know that i have to do the following things:

  1. First, I have to find the general equation of the ellipse using this method
  2. Then we should find the major and minor axis by analyzing the general equation. (the ellipse might be rotated.)
  3. Then using this method, we can find the circumference of the ellipse.

Is there any simpler way to do this?

How can I find the major and minor axis from general rotated equation?

PS: I am a computer programmer. I don't know much about pure mathematics.

Community
  • 1
Matin Lotfaliee
  • 173

1 Answers1

2

I don't know if the following method is simpler but it gives a construction to find all the points of the ellipse. This method is based on Pascal's theorem and it cannot be understood without understanding at least the statement of the said theorem.

Let's see the following figure and follow the instructions.

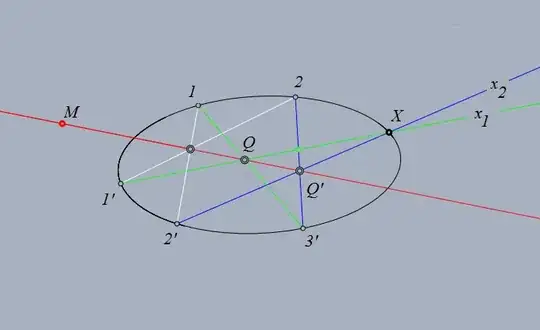
enter image description here

If you have five points then, according to Pascal's theorem, you can choose any two of them and denote them by $1$ an $2$, and denote the remaining $3$ points by $1'$,$2'$, and $3'$.

Here is the construction which will find for you all the points on the ellipse.

  1. Join $1'$ and $2$ and $1$ and $2'$ with straight lines. (White segments; only for the sake of simplicity, I drew segments.)
  2. Choose an arbitrary point $M$ (distinct from the already given ones). This point will be called the moving point.
  3. Construct the straight line joining the moving point and the intersection of of $1'2$ and $2'1.$ (red line)
  4. Join $1$ with $3'$.
  5. Find the intersection point, $Q$, of $13'$ and the red line.
  6. Connect $1'$ with $Q$. (The green ray coming from $1'$: $x_1$)
  7. Join $2$ and $3'$. (blue line)
  8. Find the intersection point of the red line and $23'$. ($Q'$)
  9. Join $2'$ and $Q'$. (the blue ray denoted by $x_2$)
  10. Find the intersection point of $x_1$ and $x_2$: $X$.

Now, $X$ is a sixth point on the ellipse. If you move the moving point $M$ around then your points on the ellipse will loom up. After one revolution you can go through the points of the ellipse again and you can watch the intersection points of the red line and the ellipse. If this distance is maximal then the red line is on the great axis...

Good luck.

zoli
  • 20,452
  • I am a programmer, with what algorithm should i place the point M around? – Matin Lotfaliee Jul 08 '15 at 07:57
  • Take a circle which contain all the five points. The center of the xircle shold be the mass center if the points. Zhe radius us greater than the farthest point. Then M would move on zhet circle. This is howI have alólready done this, Soeey for the typos. I don"t fund my glasses and type practically blind. – zoli Jul 08 '15 at 08:19