I know that we need base e to differentiate but I don't see what makes this formula work.
$$ P = P_0 e^{rt} $$
where the $P_0$ refers to initial population, $r$ the rate, and $t$ the time.
Changing the base changes the curve, so why does base $e$ work? I mean $r$ and $t$ are pretty straightforward numbers so there's no fancy constants (other than $e$). Why is it not base $2$ or something else?
Two issues: (1) Why is base $e$ used?; and (2) "Changing the base changes the curve." is wrong if you do things right.
Suppose the population doubles every $30$ years. Then what is the population after $180$ years?
Notice that $180/30=6$, i.e. $6$ is the number of $30$-year periods and thus the number of doublings. So the population will be $P_0\cdot2^6 = P_0\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2 = 64 P_0$.
What is the population after $t$ years? The number of $30$-year periods is $t/30$, so that's the number of doublings, and it is $P_0 \cdot 2^{t/30}$.
Notice that base $e$ is nowhere used above.
But what is the instantaneous rate of change at time $t=0$? It is $$ \left.\frac{dP}{dt}\right|_{t=0} = P_0 \frac d {dt} 2^{t/30} = P_0 \cdot 2^{t/30} (\log_e 2)\cdot 1 {30}. $$ If you're not dealing with instantaneous rates of change, then you don't need $e$.
Suppose now we're told the initial population is $P_0$ and it's growing at $P_0/40$ per year. How long will it take to double? It follows that $$ P= P_0 e^{t/40}. \tag 1 $$ If $t$ is the doubling time, then $e^{t/40}=2$, so $\dfrac t {40} =\log_e 2$ and the doubling time is $t=40\log_e 2 = 27.725887\ldots\text{ years}$. Again, we need $e$ only because instantaneous rates of change are involved.
Notice that $\dfrac d {dt} 8^t = (8^t\cdot\text{constant})$. If the base had been $6$ rather than $8$, the constant would be different. Only when the base is $e$ is the constant $1$. That is what is "natural" about $e$.
Above we found that the doubling time is $27.725887\ldots$ years, and the first argument above shows that $$ P = P_0 \cdot 2^{t/27.725887\ldots}. \tag 2 $$
Is $(1)$ different from $(2)$? No. They're the same. Changing the base does not change the curve if $t$ is multiplied by the constant appropriate to the base in each case.
I've seen students write things like $P = P_0 e^{-(\ln 8) t}$ and then fail to do the simplification that says this is $P = P_0\left(\frac 1 8 \right)^t$. If $t=2$, then you have $P=P_0\cdot\frac 1 {64}$, but sometimes students say $\ln 8 = 2.079$ and $e^{-(2.079)\cdot 2} = 0.015638804272$, and fail to notice that that is close to $1/64$, and think that by adding lots of digits they're making it very accurate. Those later digits are garbage. Notice that $1/64 = 0.015625$ and compare that with that previous number.
$\displaystyle P = P_0 e^{-(\ln 8) t}$ is the same as $\displaystyle P = P_0\left(\frac 1 8 \right)^t$, so changing the base doesn't change the curve if things are done correctly.
A lot of the other answers danced around the answer, so I'm going to just give you a straight one, since you said you knew a little Calculus.
If $r$ is the rate of change in a population $P$, then the actual change (in terms of the number of members) is given by $rP$. In other words, $$ \frac{dP}{dt} = rP $$ Now, to move from a dynamic equation of rates to a static equation (i.e., one without differentials) you have to integrate. That means you need to separate the variables so that they are together by themselves with their differentials. You can do that in this equation by dividing both sides by $P$ and multiplying both side by $dt$. This will yield the following equation: $$ \frac{dP}{P} = r\,dt $$ Now, we can integrate both sides: $$ \int \frac{dP}{P} = \int r\,dt $$ These are basic integral rules (remember, $r$ is a constant!). Therefore, the equation becomes: $$ \ln(P) = r\,t + C $$ However, we don't want the equation for the log of the population, we want the equation for $P$ itself, therefore we can exponentiate both sides of the equation to get: $$e^{\ln(P)} = e^{r\,t + C}$$ This then reduces to: $$ P = e^{r\,t + C} $$ Now, before going further, the actual answer to your question is now given. You have an $e$ because the integral gave you an $\ln(P)$, and exponentiation by $e$ is what converts $\ln(P)$ to just $P$.
However, to finish the equation, let's use exponent rules to reduce this further. We can convert the right-hand exponentiation to: $$ P = e^Ce^{r\,t} $$ However, $e^C$ is just a combination of constants, so it will itself be a constant that is still unknown. So, we can substitute $e^C$ with just $C$, giving us: $$ P = C\,e^{r\,t} $$ So, what is $C$? Well, sometimes you can see what something is by setting other things to zero. So, let's set $t = 0$ and see what pops out: $$ P = C\,e^{r(0)} \\ P = C\,e^{0} \\ P = C\cdot 1 \\ P = C $$ So, as you can see, $C$ is just the initial population at time $t = 0$. So, we often represent the "first" of something as $P_0$. So $C = P_0$. Now the equation becomes: $$ P = P_0 e^{r\,t} $$ This is the equation where you were wondering where it came from. Hopefully all of the pieces are now clear.
The $e$ comes from the fact that integrating $\frac{dP}{P}$ yield $\ln(P)$, but what we really wanted was $P$ itself, and exponentiating both sides with $e$ will yield that.
We define $e = \displaystyle \lim_{n\to \infty} \left(1+\dfrac{1}{n}\right)^n$. The reason it shows up, why we have this definition, is the following:
Say a population, $P_0$ doubles in a "unit" of time, $t'$ (we set this to $1$ for convenience right now). Then the population at a unit of time $t'$ is $P_0 *\left(1+\frac{1}{1}\right)$. Say you want to chop this up more say it up more, like twice. This means that at half a unit of time, you get half of the population to grow, and at full you get another half. The population is then $P_0 \left(1+\frac{1}{2}\right)^2$. In general, if you want to have your population growing $n$ times, the population in a unit of time is $\left(1+\frac{1}{n}\right)^n$
However, populations are ALWAYS growing, so you take the limit for continuously compounded population growth, and you get $e$.
Furthermore we can show that $e^{rt}=\lim\limits_{n\to\infty} \left(1+\frac{rt}{n}\right)^n$.
Now your question is, why can't we have a different base? Well the answer is that the $r$ takes care of it. Lets say you have a model:
$$P(t)=P_0 e^{rt}$$
and you want it in with a base $2$. Well simply note that $e^{rt}=(e^r)^t$. So if you want it in base $2$, let $r'=\log_2(e^{r})$. Then:
$$P(t)=P_0 e^{rt}=P_0 2^{\log_2(e^{r})t}=P_0 2^{r' t}$$
I've recently been struggling with this very question, and think I have figured it out for myself. Here's the way I came to understand it:
Couple notes:
First, much of this insight is due to Kalid Azad and Grant Sanderson.
Second, I'm describing exponential growth as a function of time here, but it could easily be a function of anything else, such as distance, etc.
Suppose you have a single individual creature, with mass $1$ kg of "active tissue", at day $0$. The creature grows in the following way: At the start of each day, the active tissue spawns new, inactive tissue, at a linear rate such that at the end of that day, the amount of new tissue is equal to that of the starting (active) tissue. And at the moment this doubling has been completed, the newly spawned tissue also becomes active.
Such a function would look like this:
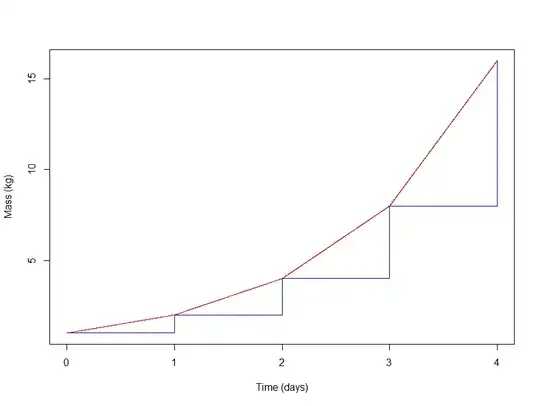
The red line shows the mass as a function of time, and the height of each blue horizontal line indicates the mass of the active tissue during that particular day. Note that the function is noncontinuous.
Next, suppose we want to consider the rate at which this function grows. There are two distinct things we could mean by "rate".
1) The relative growth rate, which is the rate the active tissue grows, relative to the mass of the active tissue. At the start of day $0$, there is $1$ kg of active tissue. At the end of day $0$, there is $1$ kg of new tissue. So the relative growth rate is ($1$ kg new tissue/$1$ kg active tissue)/$1$ day, which is $1$ unit/day, or $100\%$ growth per day.
At the start of day $1$, the newly formed tissue becomes active, so now we have $2$ kg of active tissue. At the end of day $1$, we have $2$ kg of new tissue. So the growth rate is ($2$ kg/$2$ kg)/$1$ day = $100\%$ growth/day.
What if we restrict our time period to half a day? Let's choose the start of day $1$ as our start time, and halfway through day $1$ as our end time. During this half day, we've grown $1$ kg of new tissue, and this was born of $2$ kg of active tissue. So the growth rate is ($1$ kg/$2$ kg)/$0.5$ days = $100\%$ growth/day. So, despite this strange noncontinuous function, the growth rate is a constant $100\%$ per day.
2) The time derivative of mass, $\frac{dm}{dt}$, which denotes how fast the mass is changing per unit time. We're now not asking how much it's changing proportionally, but how much the mass variable itself is changing. As such, it will be in kg/day, rather than units/day or percentage growth/day.
Notice that at any given time, $\frac{dm}{dt}$ is equal to the current amount of active tissue (i.e. the total accumulated mass at the start of that day). And this makes perfect sense - if the active tissue is growing at $100\%$ per day, then $\frac{dm}{dt}$, at any given moment, is $100\%$ of the mass of the currently active tissue. You can verify this by inspecting the graph: The height of the horizontal blue lines (position on the y-axis that they'd intersect if extended) indicates two things: the mass of active tissue during that day, and also $\frac{dm}{dt}$, or the slope, during that day. Those values are $1,2,4,8$ for the four days shown.
Also note that, unlike $\frac{dm}{dt}$, the relative growth rate is invariant. It is always $100\%$ no matter what the time is. As such, it is a particularly useful quantity, since it efficiently captures much of the information about this function. Keep this fact in mind, as it will be relevant later, when addressing your specific question.
Now, let's modify the system in a crucial way. Instead of having to wait a whole day before the new tissue becomes active, new tissue is immediately active from the moment it is born. We now have continuous $100\%$ growth/day. As a result, the total tissue at the end of the first day will be more than $1$. It will be $e$. This is the result of deriving $e$ from continuously compounding interest, as demonstrated in user223391's answer.
So $e$ is the ratio of how much you end up with to how much you started with, when you have continuous growth at a rate of $100\%$ per day, for a duration of $1$ day.
So, if under continuously compounding growth, we end up with $e$ kg at the end of the first day (starting with $1$ kg), what will be our total mass at the end of day $2$? Well, remember that we defined $e$ as the ratio of how much you end up with to how much you started with. If we start with $e$, then at the end of another unit of time, we'll have $e\cdot e$, or $e^2$. In general, the growth can be modeled by $$m=e^t$$ which represents mass as a function of time, under a regime of continuous compounding $100$ percent growth.
Side note: technically, a function can be continuous, but not continuously compounding. $y = x$ and $y = x^2$ are both continuous, but they are not continuously compounding. Any function with the form $A \cdot B^X$ is, however, continuously compounding. It's probably safe to assume that anytime you see the term "continuous growth", it means "continuously compounding growth".
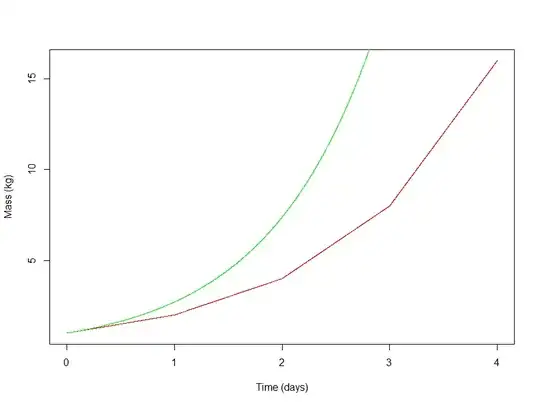
Notice that this new function (green) rises faster than the noncontinuous (red) function. This isn't surprising, given that $e$ is larger than $2$.
What about $\frac{dm}{dt}$ with this new system? Well, that's easy. It's the same as before we had continuous growth. $\frac{dm}{dt}$ is equal to the amount of active tissue that currently exists, per unit time (kg/day). Except that now, all the tissue is active! So, $\frac{dm}{dt}$ is now a continuous function, and evolves as gradually as the amount of active mass does, which is infinitely gradually! Compare this to the noncontinuous function, where $\frac{dm}{dt}$ is still equal to the amount of active tissue, but since the amount of active tissue grows discretely, so does the time derivative. Also note that in the noncontinuous case, $\frac{dm}{dt}$ is not equal to the total amount of accumulated tissue, as it is in the continuous case, since not all of the accumulated tissue is active.
So we've talked about $100\%$ growth (from here on in, "growth" means "continuous growth"). What about $50\%$ growth? How would we model that using $e$?
Well, let's work backwards. First, let's assume we can model this with $e^x$, where $x$ is a function of $t$, which we'll call $g(t)$. Somehow, $g(t)$ incorporates information about our growth rate. Under this assumption, when the growth rate is $1$, $g(t)$ must be equal to $t$. So, our more general model of growth, that isn't restricted to $100\%$ growth, is
$$m = e^{g(t)}$$
At 50% growth per day, we know that $\frac{dm}{dt}$ will be $50\%$ of the current mass (by the same logic that we know that $\frac{dm}{dt}$ of $e^t$, which is the function representing $100\%$ growth, is $100\%$ of the current mass). More generally $$\frac{dm}{dt} = \frac{d}{dt}(e^{g(t)}) = rm$$ where $r$ is the growth rate ($1$ for $100\%$, $0.5$ for $50\%$, etc.), and $m$ is mass. We also know, by the chain rule, that
$$\frac{dm}{dt} = e^{g(t)} \cdot g'(t)$$
and therefore
$$rm = e^{g(t)} \cdot g'(t)$$
Now, since $m = e^{g(t)}$
$$rm = m * g'(t)$$
$$r = g'(t)$$ Now we want to find out what $g(t)$ is, so we can find out what $x$ is (remember, we're modeling $e^x$ as $e^{g(t)}$). If we integrate both sides we get $$g(t) = rt + C$$
So $e^x$ is $e^{rt+c}$, which is equal to $e^{rt} \cdot e^C$.
$e^C$ is just another constant, $C$, and, as shown in johnnyb's answer, $C$ is the starting mass, which we choose to be $1$ for this example.
So, we are left with $$m = e^{rt}$$
This is a very cool result: It shows that we can model continuous growth (where all the tissue is active!) for any desired growth rate, and for any time, using $e^{rt}$. With $e$ as a base, the overall rate (the product of the growth rate and duration) is represented by the exponent.
Now we are ready to answer your question:
We can actually model the noncontinuous scenario (red line) using a continuous function, $2^t$ (blue line)
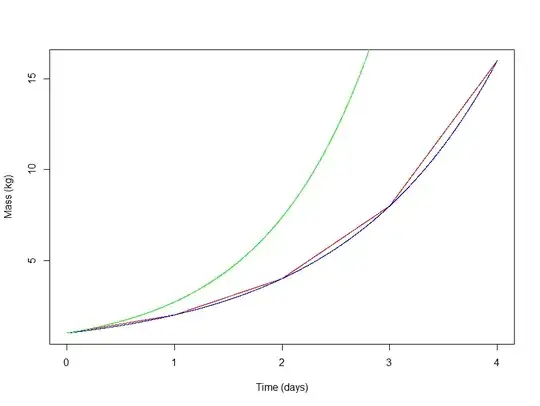
This is certainly a continuous compounding scenario, where all the tissue is active, but the growth rate is clearly less than $100\%$, since it rises slower than $e^t$ (green line). So, what is the growth rate of $2^t$? Well we can rewrite $2^t$ as follows
$$2^t = b^{\log_b (2^t)}$$ where $b$ is any arbitrary base. Let's see what happens when we pick $e$ as our base. $$2^t = e^{ln(2^t)}$$
Now, given that $ln{(2^t)} = t \cdot ln(2)$, we have $$2^t = e^{ln(2)\cdot t}$$
which means that the growth rate of $2^t$ is $ln(2)$.
Now we see why it is convenient to model population growth with base $e$ , even if we don't care about finding the time derivative. With base $e$, the rate is encoded directly in the exponent. It's explicit! With another base, $b$, we need to multiply the exponent by a constant, $ln(b)$, to calculate the rate.
Using $e$ here serves two purposes - it makes it easier to infer the growth rate of whatever function is being described. When we see $e^{rt}$, we know right away that the growth rate is $r$. And remember, the growth rate, $r$, is fundamental in describing the system - it is an invariant. Secondly, if we are trying to model a physical phenomenon, and we have actually empirically measured the growth rate or theoretically inferred it, we can readily model the phenomenon using $e^{rt}$, or indeed $A \cdot e^{rt}$.
Remember, all exponential curves belong to the same family, and any given curve can be expressed using any given base. Using base $e$ is simply a very convenient base.
Note that, according to your equation,
$$\frac{\mathrm{d}P}{\mathrm{d}t} = rP,$$ and $P(t=0) = P_0$. If $t$ indicates time and $P$ population, what is $r$? What does this equation tell us? How do you integrate it in order to get your solution?
"e" has come in by solving a differential equation for continuous growth.
It is not necessarily there in a population growth equation, which could be of the form of
P = $P_0\cdot{(1+r)}^t$ or the even more general equation y = $a\cdot b^x$
The first is is of the form of compound interest, and the second uses growth factor "b" rather than growth rate (decimals) "r"
Note that $e = \displaystyle \lim_{n\to \infty} \left(1+\dfrac{1}{n}\right)^n$, and this is the continuous growth or decay problem, then you take the limit as $n$ to infinity and get $e$.
