Can someone explain the last step in this process. Specifically, how do you get the new limits of integration?
Expected Value Definition: $E[Y] = \int_0^\infty{P\{Y \ge y\} \, dy}$
Expand: $E[Y] = \int_0^\infty{\int_y^\infty{f_Y(x) \, dx} \, dy}$
Clarify: $E[Y] = \int_{y=0}^{y=\infty}{\left(\int_{x=y}^{x=\infty}{f_Y(x) \, dx}\right) \, dy}$
Interchange order of integration: $E[Y] = \int_{x=0}^{x=\infty}{\left(\int_{y=0}^{y=x}{dy} \right) f_Y(x) \, dx}$
Assume that $f_Y$, the pdf of $Y\ge 0$, exists. In this case the expected value is
$$E[Y]=\int_{0}^{+\infty}x\ f_Y(x)\ dx$$
Also, assume that the integral above is finite.
It is obvious that $x$ can be written as
$$x=\int_0^x\ 1\ dy, \ x\ge 0.$$
With this, the expected value is
$$E[Y]=\int_{0}^{+\infty}\int_0^x\ 1\ dy\ f_Y(x)\ dx.$$
Since the expectation exists we can use Fubini' theorem so we can compute this integral as a double integral.
$$E[Y]=\iint_A1\cdot d\mu(x,y)$$ where $$A=\{(x,y): 0\le y\le x\ \text{ and } 0 \le x < \infty \}.$$ and $\mu$ is the product measure of the probability measure generated by $f_Y$ and the Lebesgue measure. (For a rectangle $r=[a,b]\times [c,d]$, the measure $\mu(r)=(b-a)\int_c^df_Y(x)\ dx$.)
The domain of the integration can be visualized:
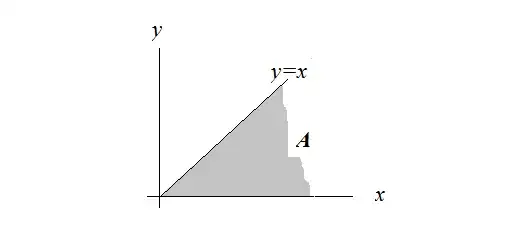
Considering the definition of $\mu$ and the shape of the domain, and referring to Fubini's theorem, the double integral above can be written as
$$\int_{0}^{+\infty}\int_{y}^{+\infty}\ 1\ f_Y(x)\ dx\ dy=$$ $$=\int_{0}^{+\infty}P(Y\ge y)\ dy.$$
