3

I have to prove the following equation by induction for $$x = \phi$$ I am stuck and I don't know how to proceed.

This is the equation

$$ \phi ^n = f_n\phi + f_{n-1} $$

where $f_n$ is the nth term of the Fibonacci sequence and $f_{n-1}$ is the (n-1)st term.

Martin Sleziak
  • 53,687
rahulgarg12342
  • 163

3 Answers3

4

One of the neat properties of $\phi$ is that $\phi^2=\phi+1$. We will use this fact later. The base step is: $\phi^1=1\times \phi+0$ where $f_1=1$ and $f_0=0$. For the inductive step, assume that $\phi^n=f_n\phi+f_{n-1}.$ Then $$\phi^{n+1}=\phi^n\phi=(f_n\phi+f_{n-1})\phi=f_n\phi^2+f_{n-1}\phi=f_n\phi+f_n+f_{n-1}\phi=(f_n+f_{n-1})\phi+f_n\\=f_{n+1}\phi+f_n.$$

Plutoro
  • 22,730
  • 3
  • 41
  • 71
3

Let me help add some insight into this problem.

You should know that $\phi$ is a root of the equation $x^2-x-1 = 0$. When we say that $\phi$ is a solution to the equation, what we mean is that if you plug in $\phi$ for $x$, you will get a true statement.

This is why $\phi^2 - \phi - 1 = 0$, or in other words, $\phi^2 = \phi + 1$.

If we were to multiply both sides of the equation by $\phi$, we now get $$ \phi^3 = \phi^2 + \phi \\ \phi^3 = (\phi + 1) + \phi = 2\phi+1 $$

Repeat: \begin{align} \phi^4 &= \phi^3 + \phi^2 \\ \phi^4 &= (2\phi + 1) + (\phi+1) = 3\phi+2 \\ \phi^5 &= \phi^4 + \phi^3 \\ \phi^5 &= (3\phi + 2) + (2\phi+1) = 5\phi+3 \\ \phi^6 &= \phi^5 + \phi^4 \\ \phi^6 &= (5\phi + 3) + (3\phi+2) = 8\phi+5 \\ \cdots &= \cdots \\ \phi^n &= \phi^{n-1} + \phi^{n-2} \end{align}

It should be much easier to imagine the induction process now.

Leucippus
  • 26,329
zhuli
  • 2,561
1

More insight:

One way to consider the basic $x^2 - x - 1 = 0$ starting point in the above answer is to consider the initial golden ratio itself, i.e., $a + b$ is to $a$ as $a$ is to $b$,

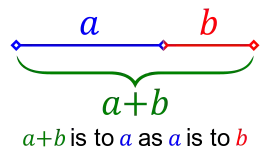
From Wikipedia's Golden Ratio

or

\begin{align*} \frac{a + b}{a} = \frac{a}{b} = \varphi. \end{align*}

Now, if $b$ is of length $1$ and $a$ is $x$, we have $a + b = 1 + x$. Then we have

\begin{align*} \frac{x + 1}{x} = \frac{x}{1} = \varphi \end{align*}

so that

\begin{align} x^2 - x - 1 = 0. \end{align}

We then can plug this into the quadratic equation

\begin{align*} \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \end{align*}

which gives

\begin{align*} \varphi = \frac{1 + \sqrt{5}}{2} = 1.6180339887498948482\dots \end{align*}

but also

\begin{align*} \varphi = \frac{1 - \sqrt{5}}{2} = -0.6180339887498948482\dots \end{align*}

but since the golden ratio is the ratio of positives, we discard the second solution$-$initially, at least. See this for a use of the conjugate.

147pm
  • 920